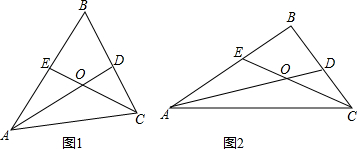
解:(1)①∵∠BAC=90°,△ADF是等腰直角三角形,
∴∠CAF+∠CAD=90°,∠BAD+∠ACD=90°,
∴∠CAF=∠BAD,
在△ACF和△ABD中,

,
∴△ACF≌△ABD(SAS),
∴CF=BD,∠ACF=∠B,
∵AB=AC,∠BAC=90°,
∴∠B=∠ACB=45°,
∴∠BCF=∠ACF+∠ACB=45°+45°=90°,
∴CF⊥BD;
②如图2,∵∠CAB=∠DAF=90°,
∴∠CAB+∠CAD=∠DAF+∠CAD,
即∠CAF=∠BAD,
在△ACF和△ABD中,

,
∴△ACF≌△ABD(SAS),
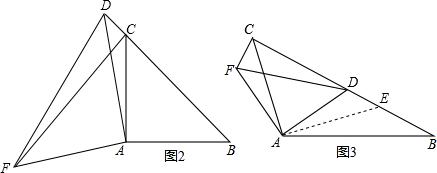
∴CF=BD,∠ACF=∠B,
∵AB=AC,∠BAC=90°,
∴∠B=∠ACB=45°,
∴∠BCF=∠ACF+∠ACB=45°+45°=90°,
∴CF⊥BD;
(2)如图3,过点A作AE⊥AC交BC于E,
∵∠BCA=45°,
∴△ACE是等腰直角三角形,
∴AC=AE,∠AED=45°,
∵∠CAF+∠CAD=90°,∠EAD+∠CAD=90°,
∴∠CAF=∠EAD,
在△ACF和△AED中,

,
∴△ACF≌△AED(SAS),
∴∠ACF=∠AED=45°,
∴∠BCF=∠ACF+∠BCA=45°+45°=90°,
∴CF⊥BD.
分析:(1)①根据同角的余角相等求出∠CAF=∠BAD,然后利用“边角边”证明△ACF和△ABD全等,根据全等三角形对应边相等可得CF=BD,全等三角形对应角相等可得∠ACF=∠B,然后求出∠BCF=90°,从而得到CF⊥BD;
②先求出∠CAF=∠BAD,然后与①的思路相同求解即可;
(2)过点A作AE⊥AC交BC于E,可得△ACE是等腰直角三角形,根据等腰直角三角形的性质可得AC=AE,∠AED=45°,再根据同角的余角相等求出∠CAF=∠EAD,然后利用“边角边”证明△ACF和△AED全等,根据全等三角形对应角相等可得∠ACF=∠AED,然后求出∠BCF=90°,从而得到CF⊥BD.
点评:本题考查了全等三角形的判定与性质,等腰直角三角形的性质,根据同角的余角相等求出两边的夹角相等是证明三角形全等的关键,此类题目的特点是各小题求解思路一般都相同.


 ,
, ,
,
 ,
,

 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案
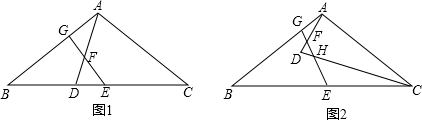 明理由.
明理由.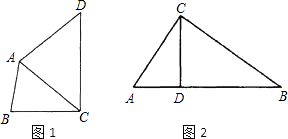
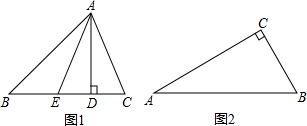 如图1,AD和AE分别是△ABC的BC边上的高和中线,点D是垂足,点E是BC的中点,规定:λA=
如图1,AD和AE分别是△ABC的BC边上的高和中线,点D是垂足,点E是BC的中点,规定:λA=