
科目:初中数学 来源: 题型:阅读理解
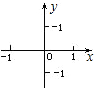 九年义务教育三年制初级中学教科书代数第三册中,有以下几段文字:“对于坐标平面内任意一点M,都有唯一的一对有序实数(x,y)和它对应;对于任意一对有序实数(x,y),在坐标平面内都有唯一的一点M和它对应,也就是说,坐标平面内的点与有序实数对是一一对应的.”“一般地,对于一个函数,如果把自变量x与函数y的每对对应值分别作为点的横坐标与纵坐标,在坐标平面内描出相应的点,这些点所组成的图形,就是这个函数的图象.”“实际上,所有一次函数的图象都是一条直线.”“因为两点确定一条直线,所以画一次函数的图象时,只要先描出两点,再连成直线,就可以了.”由此可知:满足函数关系式的有序实数对所对应的点,一定在这个函数的图象上;反之,函数图象上的点的坐标,一定满足这个函数的关系式.另外,已知直线上两点的坐标,便可求出这条直线所对应的一次函数的解析式.
九年义务教育三年制初级中学教科书代数第三册中,有以下几段文字:“对于坐标平面内任意一点M,都有唯一的一对有序实数(x,y)和它对应;对于任意一对有序实数(x,y),在坐标平面内都有唯一的一点M和它对应,也就是说,坐标平面内的点与有序实数对是一一对应的.”“一般地,对于一个函数,如果把自变量x与函数y的每对对应值分别作为点的横坐标与纵坐标,在坐标平面内描出相应的点,这些点所组成的图形,就是这个函数的图象.”“实际上,所有一次函数的图象都是一条直线.”“因为两点确定一条直线,所以画一次函数的图象时,只要先描出两点,再连成直线,就可以了.”由此可知:满足函数关系式的有序实数对所对应的点,一定在这个函数的图象上;反之,函数图象上的点的坐标,一定满足这个函数的关系式.另外,已知直线上两点的坐标,便可求出这条直线所对应的一次函数的解析式.查看答案和解析>>
科目:初中数学 来源: 题型:阅读理解
| 1 |
| 2 |
| 1 |
| 2 |
查看答案和解析>>
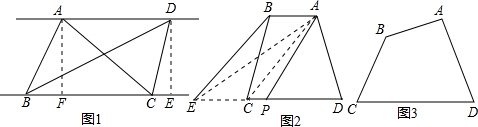
科目:初中数学 来源:1999年全国中考数学试题汇编《一次函数》(02)(解析版) 题型:解答题
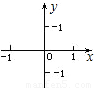
查看答案和解析>>
科目:初中数学 来源:2013年山东省青岛市中考数学模拟试卷(八)(解析版) 题型:解答题
 ×BC×AF,S△BCD=
×BC×AF,S△BCD=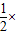 BC×DE
BC×DE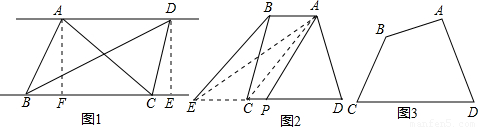
查看答案和解析>>
科目:初中数学 来源:2013年山东省青岛市中考数学模拟试卷(四)(解析版) 题型:解答题
 ×BC×AF,S△BCD=
×BC×AF,S△BCD=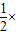 BC×DE
BC×DE
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com