

分析 (1)根据直角三角形两锐角互余即可解答;
(2)设∠ACP=α,可求出∠ACQ=60°-α,由CA∥EQ,得到∠EQC=120°+α,易证四边形EDFQ是矩形,可知∠EQF=90°,又在Rt△BQC中,∠BQC=90°-α,可知∠BQF=360°-∠EQC-∠EQF-∠BQC=60°,故∠BQF的值不会随点P的运动而改变大小,始终为一定值.
(3)线段PA的长为m,用m表示出EQ,根据S=$\frac{1}{2}$AP•EQ,可得到S与m的函数关系式,然后用二次函数的性质求出最大值.
解答 解:(1)∵AC⊥l,
∴∠CAP=90°,
又∵∠ACP=20°,
∴∠APC=70°,
由旋转的性质可知∠BQC=∠APC,
∴∠BQC=70°;
(2)∠BQF的值不会随着点P的运动而改变;理由如下:
∵△ABC是正三角形,
∴∠ACB=60°,
由旋转的性质可知∠ACP=∠BCQ,
∴∠PCQ=∠ACB=60°,
设∠ACP=α,
∴∠ACQ=60°-α,
∵AC⊥l,EQ⊥l,
∴AC∥EQ,
∴∠CEQ=180°-(60°-α)=120°+α,
又∵BD⊥l,QE⊥l,QF⊥BD,
∴四边形DEQF是矩形,
∴∠EQF=90°,
又∵∠BQC=∠APC=90°-α,
∠BQF=360°-90°-(120°+α)-(90°-α)=60°;
∴∠BQF的值不会随点P的运动而改变大小,始终为一定值,此定值为60°;
(3)∵AP=4,BD⊥l,∠BAD=90°-60°=30°,
∴BD=$\frac{1}{2}$AB=2,
∵QB=AP=m,BD⊥QF,∠BQF=60°,
∴BF=$\frac{\sqrt{3}}{2}$m,又四边形DEQF是矩形,
∴EQ=DF=2-$\frac{\sqrt{3}}{2}$m,
∴S=$\frac{1}{2}$AP•EQ=$\frac{1}{2}$m(2-$\frac{\sqrt{3}}{2}$m),
即S=-$\frac{\sqrt{3}}{4}$m2+m(0≤m≤$\frac{4\sqrt{3}}{3}$),
当m=-$\frac{1}{2×(-\frac{\sqrt{3}}{4})}$=$\frac{2\sqrt{3}}{3}$时,
∵-$\frac{\sqrt{3}}{4}$<0,0<$\frac{2\sqrt{3}}{3}$<$\frac{4\sqrt{3}}{3}$,
∴S有最大值,最大值为$\frac{\sqrt{3}}{3}$.
点评 本题是几何变换综合题目,考查了等边三角形的性质、旋转的性质、直角三角形的性质、矩形的判定与性质、三角形面积的计算、二次函数的最值等知识;本题综合性强,有一定难度.


 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案科目:初中数学 来源: 题型:填空题
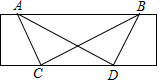 已知:如图,直尺的宽度为2cm,A、B两点在直尺的一条边上,AB=8cm,C、D两点在直尺的另一条边上.若∠ACB=∠ADB=90°,则C、D两点之间的距离为4$\sqrt{3}$cm.
已知:如图,直尺的宽度为2cm,A、B两点在直尺的一条边上,AB=8cm,C、D两点在直尺的另一条边上.若∠ACB=∠ADB=90°,则C、D两点之间的距离为4$\sqrt{3}$cm.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
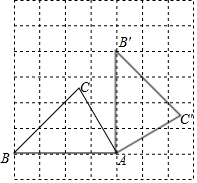 如图,△ABC的顶点A,B都在格点上,将△ABC绕点A顺时针旋转得到相应的△AB′C′,且点B的对应点B′也在格点上,则∠CAC′的度数为90°.
如图,△ABC的顶点A,B都在格点上,将△ABC绕点A顺时针旋转得到相应的△AB′C′,且点B的对应点B′也在格点上,则∠CAC′的度数为90°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (1+40%)×30%x | B. | (1+40%)(1-30%)x | C. | $\frac{x}{(1+40%)×30%}$ | D. | $\frac{x}{(1+40%)(1-30%)}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com