
°ĺŐ‚ńŅ°Ņ»ÁÕľ£¨“—÷™O «÷ĪŌŖAB…Ō“ĽĶ„£¨°ŌBOC£ľ90°„£¨»żĹ«įŚ£®MON£©Ķń÷ĪĹ«∂•Ķ„¬š‘ŕĶ„Oī¶Ō÷Ĺ껿ūįŚ»∆◊ŇĶ„O–ż◊™£¨≤ĘĪ£≥÷OMļÕOC‘ŕ÷ĪŌŖABĶńÕ¨“Ľ≤ŗ£ģ
£®1£©»Ű°ŌBOC£Ĺ50°„
ĘŔĶĪOM∆Ĺ∑÷°ŌBOC Ī£¨«ů°ŌAONĶń∂» ż£ģ
ĘŕĶĪOM‘ŕ°ŌBOCńŕ≤Ņ£¨«“°ŌAON£Ĺ3°ŌCOM Ī£¨«ů°ŌCONĶń∂» ż£ļ
£®2£©ĶĪ°ŌCOM£Ĺ2°ŌAON Ī£¨«ŽĽ≠≥Ų ĺ“‚Õľ£¨≤¬ŌŽ°ŌAOM”Ž°ŌBOCĶń żŃŅĻōŌĶ£¨≤ĘňĶ√ųņŪ”…£ģ
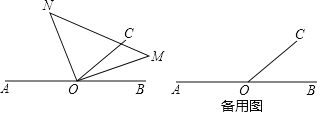
°ĺīūįł°Ņ£®1£©ĘŔ65°„£ĽĘŕ70°„£Ľ£®2£©ÕľŌÍľŻĹ‚őŲ£¨3°ŌAOM+°ŌBOC£Ĺ360°„ĽÚ°ŌAOM£Ĺ°ŌBOC£ģ
°ĺĹ‚őŲ°Ņ
£®1£©ĘŔłýĺ›∆ĹĹ«Ķń∂®“ŚĶ√ĶĹ°ŌAOC£Ĺ180°„©Ā°ŌBOC£Ĺ180°„©Ā50°„£Ĺ130°„£¨łýĺ›Ĺ«∆Ĺ∑÷ŌŖĶń∂®“ŚĶ√ĶĹ°ŌCOM£Ĺ![]() °ŌBOC£Ĺ25°„£¨”ŕ «Ķ√ĶĹĹŠ¬Ř£Ľ
°ŌBOC£Ĺ25°„£¨”ŕ «Ķ√ĶĹĹŠ¬Ř£Ľ
Ęŕ»ÁÕľ1£¨…Ť°ŌCOM£Ĺ¶Ń£¨‘Ú°ŌAON£Ĺ3¶Ń£¨«ůĶ√°ŌBOM£Ĺ50°„©Ā¶Ń£¨Ń–∑Ĺ≥ŐľīŅ…Ķ√ĶĹĹŠ¬Ř£Ľ
£®2£©ĘŔ»ÁÕľ2£¨…Ť°ŌAON£Ĺ¶Ń£¨‘Ú°ŌCOM£Ĺ2¶Ń£¨Ęŕ»ÁÕľ3£¨…Ť°ŌAON£Ĺ¶Ń£¨‘Ú°ŌCOM£Ĺ2¶Ń£¨ĘŘ»ÁÕľ4£¨…Ť°ŌAON£Ĺ¶Ń£¨‘Ú°ŌCOM£Ĺ2¶Ń£¨łýĺ›Ĺ«ĶńļÕ≤ÓľīŅ…Ķ√ĶĹĹŠ¬Ř£ģ
Ĺ‚£ļ£®1£©ĘŔ°Ŗ°ŌAOC£Ĺ180°„©Ā°ŌBOC£Ĺ180°„©Ā50°„£Ĺ130°„£¨
°ŖOM∆Ĺ∑÷°ŌBOC£¨
°ŗ°ŌCOM£Ĺ![]() °ŌBOC £Ĺ25°„£¨
°ŌBOC £Ĺ25°„£¨
°Ŗ°ŌMON£Ĺ90°„£¨
°ŗ°ŌCON£Ĺ90°„©Ā25°„£Ĺ65°„£¨
°ŗ°ŌAON£Ĺ°ŌAOC©Ā°ŌCON£Ĺ65°„£Ľ
Ęŕ»ÁÕľ1£¨°Ŗ°ŌAON£Ĺ3°ŌCOM£¨
°ŗ…Ť°ŌCOM£Ĺ¶Ń£¨‘Ú°ŌAON£Ĺ3¶Ń£¨
°ŗ°ŌBOM£Ĺ50°„©Ā¶Ń£¨
°Ŗ°ŌMON£Ĺ90°„£¨
°ŗ°ŌAON+°ŌBOM£Ĺ90°„£¨
°ŗ3¶Ń+50°„©Ā¶Ń£Ĺ90°„£¨
°ŗ¶Ń£Ĺ20°„£¨
°ŗ°ŌCON£Ĺ90°„©Ā¶Ń£Ĺ70°„£Ľ
£®2£©ĘŔ»ÁÕľ2£¨°Ŗ°ŌCOM£Ĺ2°ŌAON£¨
°ŗ…Ť°ŌAON£Ĺ¶Ń£¨‘Ú°ŌCOM£Ĺ2¶Ń£¨
°Ŗ°ŌMON£Ĺ90°„£¨
°ŗ°ŌBOM£Ĺ90°„©Ā°ŌAON£Ĺ90°„©Ā¶Ń£¨
°ŗ°ŌBOC£Ĺ°ŌBOM+°ŌCOM£Ĺ90°„©Ā¶Ń+2¶Ń£Ĺ90°„+¶Ń£¨
°Ŗ°ŌBOC£ľ90°„£¨
°ŗ’‚÷÷«ťŅŲ≤Ľīś‘ŕ£Ľ
Ęŕ»ÁÕľ3£¨°Ŗ°ŌCOM£Ĺ2°ŌAON£¨
°ŗ…Ť°ŌAON£Ĺ¶Ń£¨‘Ú°ŌCOM£Ĺ2¶Ń£¨
°Ŗ°ŌMON£Ĺ90°„£¨
°ŗ°ŌAOM£Ĺ90°„+¶Ń£¨°ŌBOC£Ĺ90°„©Ā3¶Ń£¨
°ŗ3°ŌAOM+°ŌBOC£Ĺ360°„£Ľ
ĘŘ»ÁÕľ4£¨°Ŗ°ŌCOM£Ĺ2°ŌAON£¨
°ŗ…Ť°ŌAON£Ĺ¶Ń£¨‘Ú°ŌCOM£Ĺ2¶Ń£¨
°Ŗ°ŌMON£Ĺ90°„£¨
°ŗ°ŌAOM£Ĺ90°„©Ā¶Ń£¨°ŌBOC£Ĺ180°„©Ā°ŌAOM©Ā°ŌCOM£Ĺ90°„©Ā¶Ń£¨
°ŗ°ŌAOM£Ĺ°ŌBOC£ģ






 √Ż–£Õ®––÷§”––ß◊ų“ĶŌĶŃ–īūįł
√Ż–£Õ®––÷§”––ß◊ų“ĶŌĶŃ–īūįł
| ńÍľ∂ | łŖ÷–Ņő≥Ő | ńÍľ∂ | ≥ű÷–Ņő≥Ő |
| łŖ“Ľ | łŖ“Ľ√‚∑—Ņő≥ŐÕ∆ľŲ£° | ≥ű“Ľ | ≥ű“Ľ√‚∑—Ņő≥ŐÕ∆ľŲ£° |
| łŖ∂Ģ | łŖ∂Ģ√‚∑—Ņő≥ŐÕ∆ľŲ£° | ≥ű∂Ģ | ≥ű∂Ģ√‚∑—Ņő≥ŐÕ∆ľŲ£° |
| łŖ»ż | łŖ»ż√‚∑—Ņő≥ŐÕ∆ľŲ£° | ≥ű»ż | ≥ű»ż√‚∑—Ņő≥ŐÕ∆ľŲ£° |
Ņ∆ńŅ£ļ≥ű÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°Ņ£®1£©»ÁÕľ1£¨‘ŕ![]() ÷–£¨∑÷Īū“‘
÷–£¨∑÷Īū“‘![]() °Ę
°Ę![]() ő™–ĪĪŖ£¨ŌÚ
ő™–ĪĪŖ£¨ŌÚ![]() Ķń–őÕ‚◊ųĶ»—Ł÷ĪĹ«»żĹ«–ő£¨÷ĪĹ«Ķń∂•Ķ„∑÷Īūő™
Ķń–őÕ‚◊ųĶ»—Ł÷ĪĹ«»żĹ«–ő£¨÷ĪĹ«Ķń∂•Ķ„∑÷Īūő™![]() £¨Ķ„
£¨Ķ„![]() ∑÷Īūő™
∑÷Īūő™![]() ĪŖĶń÷–Ķ„.ő £ļ
ĪŖĶń÷–Ķ„.ő £ļ ![]() «∑Ů»ęĶ»£Ņ____£®ŐÓ°į «°ĪĽÚ°į∑Ů°Ī£©£Ľ
«∑Ů»ęĶ»£Ņ____£®ŐÓ°į «°ĪĽÚ°į∑Ů°Ī£©£Ľ
£®2£©»ÁÕľ2£¨‘ŕ![]() ÷–£¨∑÷Īū“‘
÷–£¨∑÷Īū“‘![]() ő™Ķ◊ĪŖ£¨ŌÚ
ő™Ķ◊ĪŖ£¨ŌÚ![]() Ķń–őÕ‚◊ųĶ»—Ł»żĹ«–ő£¨∂•Ĺ«Ķń∂•Ķ„∑÷Īūő™
Ķń–őÕ‚◊ųĶ»—Ł»żĹ«–ő£¨∂•Ĺ«Ķń∂•Ķ„∑÷Īūő™![]() £¨«“
£¨«“![]() .Ķ„
.Ķ„![]() ∑÷Īūő™
∑÷Īūő™![]()
![]() ĪŖĶń÷–Ķ„.
ĪŖĶń÷–Ķ„.
ĘŔ ‘Ň–∂Ō![]() «∑٬ķ◊„£®1£©÷–ĶńĻōŌĶ£Ņ»Ű¬ķ◊„£¨«ŽňĶ√ųņŪ”…£Ľ»Ű≤Ľ¬ķ◊„£¨«Ž–ī
«∑٬ķ◊„£®1£©÷–ĶńĻōŌĶ£Ņ»Ű¬ķ◊„£¨«ŽňĶ√ųņŪ”…£Ľ»Ű≤Ľ¬ķ◊„£¨«Ž–ī![]() ÷ģľšīś‘ŕĶń“Ľ÷÷ĻōŌĶ£¨≤Ęľ”“‘ňĶ√ų.
÷ģľšīś‘ŕĶń“Ľ÷÷ĻōŌĶ£¨≤Ęľ”“‘ňĶ√ų.
Ęŕ»Ű![]() £¨
£¨ ![]() £¨
£¨ ![]() Ķń√śĽżő™32£¨«ů
Ķń√śĽżő™32£¨«ů![]() Ķń√śĽż.
Ķń√śĽż.

≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļ≥ű÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°Ņ»ÁÕľ1£¨Ķ„A°ĘD «Ň◊őÔŌŖ![]() …ŌŃĹ∂ĮĶ„£¨Ķ„B°ĘC‘ŕx÷Š…Ō£¨«“ňńĪŖ–őABCD «ĺō–ő£¨Ķ„E «Ň◊őÔŌŖ”Žy÷ŠĶńĹĽĶ„£¨Ń¨Ĺ”BEĹĽAD”ŕĶ„F£¨AD”Žy÷ŠĶńĹĽĶ„ő™Ķ„G£ģ…ŤĶ„AĶńļŠ◊ÝĪÍő™a(0<a<1).
…ŌŃĹ∂ĮĶ„£¨Ķ„B°ĘC‘ŕx÷Š…Ō£¨«“ňńĪŖ–őABCD «ĺō–ő£¨Ķ„E «Ň◊őÔŌŖ”Žy÷ŠĶńĹĽĶ„£¨Ń¨Ĺ”BEĹĽAD”ŕĶ„F£¨AD”Žy÷ŠĶńĹĽĶ„ő™Ķ„G£ģ…ŤĶ„AĶńļŠ◊ÝĪÍő™a(0<a<1).
(1) »Űĺō–őABCDĶń÷‹≥§ő™3.5£¨«ůaĶń÷Ķ£Ľ
(2) «ů÷§£ļ≤Ľ¬ŘĶ„A»Áļő‘ň∂Į£¨°ŌEAD£Ĺ°ŌABE£Ľ
(3) »Ű°ųABE «Ķ»—Ł»żĹ«–ő£¨
ĘŔ«ůĶ„AĶń◊ÝĪÍ£Ľ
Ęŕ»ÁÕľ2£¨»ŰĹę÷ĪŌŖBA»∆Ķ„Bįīńś Ī’Ž∑ĹŌÚ–ż◊™÷Ń÷ĪŌŖl£¨…ŤĶ„A°ĘCĶĹ÷ĪŌŖlĶńĺŗņŽ∑÷Īūő™![]() °Ę
°Ę![]() £¨«ů
£¨«ů![]() Ķń◊Óīů÷Ķ.
Ķń◊Óīů÷Ķ.
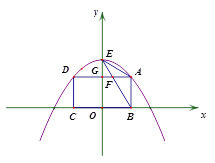
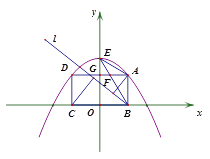
Õľ1 Õľ2
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļ≥ű÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°ŅAD”ŽBE «°ųABCĶńĹ«∆Ĺ∑÷ŌŖ£¨D£¨E∑÷Īū‘ŕBC£¨AC…Ō£¨»ŰAD=AB£¨BE=BC£¨‘Ú°ŌC=£®°°°°£©

A. 69°„ B. ![]() C.
C. ![]() D. ≤Ľń‹»∑∂®
D. ≤Ľń‹»∑∂®
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļ≥ű÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°Ņő Ő‚Ī≥ĺį£ļő“√«—ßŌįĶ»ĪŖ»żĹ«–ő ĪĶ√ĶĹ÷ĪĹ«»żĹ«–őĶń“ĽłŲ–‘÷ £ļ‘ŕ÷ĪĹ«»żĹ«–ő÷–£¨»ÁĻŻ“ĽłŲ»ŮĹ«Ķ»”ŕ30°„£¨ń«√īňŁňý∂‘Ķń÷ĪĹ«ĪŖĶ»”ŕ–ĪĪŖĶń“ĽįŽ£ģľī£ļ»ÁÕľ1£¨‘ŕRt°ųABC÷–£¨°ŌACB=90°„£¨°ŌABC=30°„£¨‘Ú£ļAC=![]() AB£ģ
AB£ģ

ŐĹĺŅĹŠ¬Ř£ļ–°√ųÕ¨—ß∂‘“‘…ŌĹŠ¬Ř◊ųŃňĹÝ“Ľ≤Ĺ—–ĺŅ£ģ
£®1£©»ÁÕľ1£¨Ń¨Ĺ”ABĪŖ…Ō÷–ŌŖCE£¨”…”ŕCE=![]() AB£¨“◊Ķ√ĹŠ¬Ř£ļĘŔ°ųACEő™Ķ»ĪŖ»żĹ«–ő£ĽĘŕBE”ŽCE÷ģľšĶń żŃŅĻōŌĶő™°°°°£ģ
AB£¨“◊Ķ√ĹŠ¬Ř£ļĘŔ°ųACEő™Ķ»ĪŖ»żĹ«–ő£ĽĘŕBE”ŽCE÷ģľšĶń żŃŅĻōŌĶő™°°°°£ģ
£®2£©»ÁÕľ2£¨Ķ„D «ĪŖCB…Ō»ő“‚“ĽĶ„£¨Ń¨Ĺ”AD£¨◊ųĶ»ĪŖ°ųADE£¨«“Ķ„E‘ŕ°ŌACBĶńńŕ≤Ņ£¨Ń¨Ĺ”BE£ģ ‘ŐĹĺŅŌŖ∂őBE”ŽDE÷ģľšĶń żŃŅĻōŌĶ£¨–ī≥Ųń„Ķń≤¬ŌŽ≤Ęľ”“‘÷§√ų£ģ
£®3£©ĶĪĶ„Dő™ĪŖCB—”≥§ŌŖ…Ō»ő“‚“ĽĶ„ Ī£¨‘ŕ£®2£©ŐűľĢĶńĽýī°…Ō£¨ŌŖ∂őBE”ŽDE÷ģľšīś‘ŕ‘ű—ýĶń żŃŅĻōŌĶ£Ņ«Ž÷ĪĹ”–ī≥Ųń„ĶńĹŠ¬Ř°°°°£ģ
Õō’Ļ”¶”√£ļ»ÁÕľ3£¨‘ŕ∆Ĺ√ś÷ĪĹ«◊ÝĪÍŌĶxOy÷–£¨Ķ„AĶń◊ÝĪÍő™£®©Ā![]() £¨1£©£¨Ķ„B «x÷Š’żįŽ÷Š…ŌĶń“Ľ∂ĮĶ„£¨“‘ABő™ĪŖ◊ųĶ»ĪŖ°ųABC£¨ĶĪCĶ„‘ŕĶŕ“ĽŌůŌřńŕ£¨«“B£®2£¨0£© Ī£¨«ůCĶ„Ķń◊ÝĪÍ£ģ
£¨1£©£¨Ķ„B «x÷Š’żįŽ÷Š…ŌĶń“Ľ∂ĮĶ„£¨“‘ABő™ĪŖ◊ųĶ»ĪŖ°ųABC£¨ĶĪCĶ„‘ŕĶŕ“ĽŌůŌřńŕ£¨«“B£®2£¨0£© Ī£¨«ůCĶ„Ķń◊ÝĪÍ£ģ
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļ≥ű÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°ŅĹŕ‘ľ”√ňģ «ő“√«Ķń√ņĶ¬£¨ňģŃķÕ∑ĻōĪ’≤Ľ—ŌĽŠ‘ž≥…Ķőňģ£¨»›∆ųńŕ Ęňģ![]() ”ŽĶőňģ Īľš
”ŽĶőňģ Īľš![]() ĶńĻōŌĶ”√Ņ…“‘Ō‘ ĺňģŃŅĶń»›∆ų◊Ų»ÁÕľ
ĶńĻōŌĶ”√Ņ…“‘Ō‘ ĺňģŃŅĶń»›∆ų◊Ų»ÁÕľ![]() Ķń ‘—ť£¨≤Ęłýĺ› ‘—ť żĺ›Ľś÷∆≥Ų»ÁÕľ
Ķń ‘—ť£¨≤Ęłýĺ› ‘—ť żĺ›Ľś÷∆≥Ų»ÁÕľ![]() ĶńļĮ żÕľŌů£¨ĹŠļŌÕľŌůĹ‚īūŌ¬Ń–ő Ő‚£ģ
ĶńļĮ żÕľŌů£¨ĹŠļŌÕľŌůĹ‚īūŌ¬Ń–ő Ő‚£ģ
£®![]() £©»›∆ųńŕ‘≠”–ňģ∂ŗ…Ŕ…ż£ģ
£©»›∆ųńŕ‘≠”–ňģ∂ŗ…Ŕ…ż£ģ
£®![]() £©«ů
£©«ů![]() ”Ž
”Ž![]() ÷ģľšĶńļĮ żĻōŌĶ Ĺ£¨≤Ęľ∆ň„‘ŕ’‚÷÷Ķőňģ◊īŐ¨Ō¬“ĽŐžĶńĶőňģŃŅ «∂ŗ…Ŕ…ż£ģ
÷ģľšĶńļĮ żĻōŌĶ Ĺ£¨≤Ęľ∆ň„‘ŕ’‚÷÷Ķőňģ◊īŐ¨Ō¬“ĽŐžĶńĶőňģŃŅ «∂ŗ…Ŕ…ż£ģ


≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļ≥ű÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
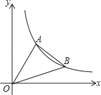
°ĺŐ‚ńŅ°Ņ»ÁÕľ£¨÷ĪŌŖy=![]() x”Ž∑īĪ»ņżļĮ żĶńÕľŌůĹĽ”ŕĶ„A£®3£¨a£©£¨Ķŕ“ĽŌůŌřńŕĶńĶ„B‘ŕ’‚łŲ∑īĪ»ņżļĮ żÕľŌů…Ō£¨OB”Žx÷Š’żįŽ÷ŠĶńľ–Ĺ«ő™¶Ń£¨«“tan¶Ń=
x”Ž∑īĪ»ņżļĮ żĶńÕľŌůĹĽ”ŕĶ„A£®3£¨a£©£¨Ķŕ“ĽŌůŌřńŕĶńĶ„B‘ŕ’‚łŲ∑īĪ»ņżļĮ żÕľŌů…Ō£¨OB”Žx÷Š’żįŽ÷ŠĶńľ–Ĺ«ő™¶Ń£¨«“tan¶Ń=![]() £ģ
£ģ
£®1£©«ů∑īĪ»ņżļĮ żĶńĹ‚őŲ Ĺ£Ľ
£®2£©«ůĶ„BĶń◊ÝĪÍ£Ľ
£®3£©«ůS°ųOAB£ģ
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļ≥ű÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°Ņ“‘ŌŖ∂őACő™∂‘Ĺ«ŌŖĶńňńĪŖ–őABCD(ňŁĶńňńłŲ∂•Ķ„A£¨B£¨C£¨Dįīň≥ Ī’Ž∑ĹŌÚŇŇŃ–)£¨“—÷™AB£ĹBC£ĹCD£¨°ŌABC£Ĺ100°„£¨°ŌCAD£Ĺ40°„£¨‘Ú°ŌBCDĶń∂» żő™________£ģ
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļ≥ű÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°Ņ»ÁÕľ£¨∆Ĺ––ňńĪŖ–őABCD÷–£¨Ķ„Eő™BCĪŖ…Ō“ĽĶ„£¨AEļÕBDĹĽ”ŕĶ„F£¨“—÷™°ųABFĶń√śĽżĶ»”ŕ 6,°ųBEFĶń√śĽżĶ»”ŕ4£¨‘ÚňńĪŖ–őCDFEĶń√śĽżĶ»”ŕ___________

≤ťŅīīūįłļÕĹ‚őŲ>>
įŔ∂»÷¬–Ň - Ń∑Ōį≤ŠŃ–ĪŪ - ‘Ő‚Ń–ĪŪ
ļĢĪĪ °Ľ•Ń™ÕÝő•∑®ļÕ≤ĽŃľ–ŇŌĘĺŔĪ®∆ĹŐ® | ÕÝ…Ō”–ļ¶–ŇŌĘĺŔĪ®◊®«Ý | ĶÁ–Ň’©∆≠ĺŔĪ®◊®«Ý | …śņķ ∑–ťőř÷ų“Ś”–ļ¶–ŇŌĘĺŔĪ®◊®«Ý | …ś∆ů«÷»®ĺŔĪ®◊®«Ý
ő•∑®ļÕ≤ĽŃľ–ŇŌĘĺŔĪ®ĶÁĽį£ļ027-86699610 ĺŔĪ®” Ōš£ļ58377363@163.com