
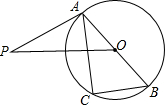
 如图,已知AB是⊙O的直径,OP垂直于弦AC,PA是⊙O的切线,求证:△ABC∽△POA.
如图,已知AB是⊙O的直径,OP垂直于弦AC,PA是⊙O的切线,求证:△ABC∽△POA. 科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在一条笔直的公路的同侧依次排列着A,C,B三个村庄,某天甲、乙两车分别从A,B两地出发,沿这条公路匀速行驶至C地停止,从甲车出发至甲车到达C地的过程,甲、乙两车各自与C地的距离y(km)与甲车行驶时间t(h)之间的函数关系如图所示.
在一条笔直的公路的同侧依次排列着A,C,B三个村庄,某天甲、乙两车分别从A,B两地出发,沿这条公路匀速行驶至C地停止,从甲车出发至甲车到达C地的过程,甲、乙两车各自与C地的距离y(km)与甲车行驶时间t(h)之间的函数关系如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在平面直角坐标系中,O为坐标原点,抛物线F:y=ax2+2ax+c经过A(-4,0),B(0,4)两点,与x轴交于另一点C,直线y=x+5与x轴交于点D,与y轴交于点E.
如图,在平面直角坐标系中,O为坐标原点,抛物线F:y=ax2+2ax+c经过A(-4,0),B(0,4)两点,与x轴交于另一点C,直线y=x+5与x轴交于点D,与y轴交于点E.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知AB是⊙O的直径,C是⊙O上一点,∠BAC的平分线交⊙O于点D,交⊙O的切线BE于点E,过点D作DF⊥AC,交AC的延长线于点F.
如图,已知AB是⊙O的直径,C是⊙O上一点,∠BAC的平分线交⊙O于点D,交⊙O的切线BE于点E,过点D作DF⊥AC,交AC的延长线于点F.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,某小区楼房附近有一个斜坡,小张发现楼房在水平地面与斜坡处形成的投影中,在斜坡上的影子长CD=6m,坡角到楼房的距离CB=8m.在D点处观察点A的仰角为60°,已知坡角为30°,你能求出楼房AB的高度吗?
如图,某小区楼房附近有一个斜坡,小张发现楼房在水平地面与斜坡处形成的投影中,在斜坡上的影子长CD=6m,坡角到楼房的距离CB=8m.在D点处观察点A的仰角为60°,已知坡角为30°,你能求出楼房AB的高度吗?查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图所示,某人从甲地出发,骑摩托车去乙地,途中因车出现故障而停车修理,到达乙地时正好用了2小时,已知摩托车行驶的路程s(千米)与行驶的时间t(时)之间的函数关系由下面的图象OBCD给出,若这辆摩托车平均每行驶100千米的耗油量为2升,则从甲地到乙地,这辆摩托车耗油量为0.9升,车修好后,摩托车的速度为30千米/小时.
如图所示,某人从甲地出发,骑摩托车去乙地,途中因车出现故障而停车修理,到达乙地时正好用了2小时,已知摩托车行驶的路程s(千米)与行驶的时间t(时)之间的函数关系由下面的图象OBCD给出,若这辆摩托车平均每行驶100千米的耗油量为2升,则从甲地到乙地,这辆摩托车耗油量为0.9升,车修好后,摩托车的速度为30千米/小时.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com