
【题目】 抛物线![]() 与
与![]() 轴交于点
轴交于点![]() (
(![]() 在
在![]() 的左侧),与
的左侧),与![]() 轴交于点
轴交于点![]() .
.
⑴求直线![]() 的解析式;
的解析式;
⑵抛物线的对称轴上存在点![]() ,使
,使![]() ,利用图
,利用图![]() 求点
求点![]() 的坐标;
的坐标;
⑶点![]() 在
在![]() 轴右侧的抛物线上,利用图
轴右侧的抛物线上,利用图![]() 比较
比较![]() 与
与![]() 的大小,并说明理由.
的大小,并说明理由.
【答案】(1)y=﹣x+3;(2)(1,2+2![]() )或(1,﹣2﹣2
)或(1,﹣2﹣2![]() ),(3)当Q点横坐标为5时,∠OCA=∠OCQ;当Q点横坐标大于5时,则∠OCQ逐渐变小,故∠OCA>∠OCQ;当Q点横坐标小于5且大于0时,则∠OCQ逐渐变大,故∠OCA<∠OCQ..
),(3)当Q点横坐标为5时,∠OCA=∠OCQ;当Q点横坐标大于5时,则∠OCQ逐渐变小,故∠OCA>∠OCQ;当Q点横坐标小于5且大于0时,则∠OCQ逐渐变大,故∠OCA<∠OCQ..
【解析】
试题分析:.(1)由抛物线解析式可求得B、C的坐标,利用待定系数法可求得直线BC的解析式;
(2)由直线BC解析式可知∠APB=∠ABC=45°,设抛物线对称轴交直线BC于点D,交x轴于点E,结合二次函数的对称性可求得PD=BD,在Rt△BDE中可求得BD,则可求得PE的长,可求得P点坐标;
(3)设Q(x,﹣x2+2x+3),当∠OCQ=∠OCA时,利用两角的正切值相等可得到关于x的方程,可求得Q点的横坐标,再结合图形可比较两角的大小.
试题解析:(1)在y=﹣x2+2x+3中,令y=0可得0=﹣x2+2x+3,解得x=﹣1或x=3,令x=0可得y=3,
∴B(3,0),C(0,3),∴可设直线BC的解析式为y=kx+3,
把B点坐标代入可得3k+3=0,解得k=﹣1,∴直线BC解析式为y=﹣x+3;
(2)∵OB=OC,∴∠ABC=45°,
∵y=﹣x2+2x+3=﹣(x﹣1)2+4,∴抛物线对称轴为x=1,
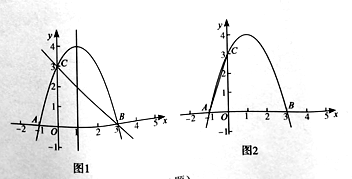
设抛物线对称轴交直线BC于点D,交x轴于点E,当点P在x轴上方时,如图1,

∵∠APB=∠ABC=45°,且PA=PB,
∴∠PBA=![]() ,∠DPB=
,∠DPB=![]() ∠APB=22.5°,
∠APB=22.5°,
∴∠PBD=67.5°﹣45°=22.5°,∴∠DPB=∠DBP,∴DP=DB,
在Rt△BDE中,BE=DE=2,由勾股定理可求得BD=2![]() ,
,
∴PE=2+2![]() ,∴P(1,2+2
,∴P(1,2+2![]() );
);
当点P在x轴下方时,由对称性可知P点坐标为(1,﹣2﹣2![]() );
);
综上可知P点坐标为(1,2+2![]() )或(1,﹣2﹣2
)或(1,﹣2﹣2![]() );
);
(3)设Q(x,﹣x2+2x+3),当点Q在x轴下方时,如图2,过Q作QF⊥y轴于点F,

当∠OCA=∠OCQ时,则△QEC∽△AOC,
∴![]() ,即
,即![]() ,解得x=0(舍去)或x=5,
,解得x=0(舍去)或x=5,
∴当Q点横坐标为5时,∠OCA=∠OCQ;
当Q点横坐标大于5时,则∠OCQ逐渐变小,故∠OCA>∠OCQ;
当Q点横坐标小于5且大于0时,则∠OCQ逐渐变大,故∠OCA<∠OCQ.


 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案科目:初中数学 来源: 题型:
【题目】如图,已知AC⊥BC,垂足为C,AC=4,BC=3 ![]() ,将线段AC绕点A按逆时针方向旋转60°,得到线段AD,连接DC,DB.
,将线段AC绕点A按逆时针方向旋转60°,得到线段AD,连接DC,DB. 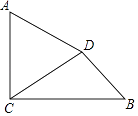
(1)线段DC=;
(2)求线段DB的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一种水果的进价为每千克3.8元,在正常的销售过程中,估计有5%的水果损耗,为保证此次销售不亏本,商家要把水果的单价至少定为_______元.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题满分8分)
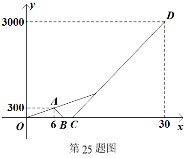
为营造书香家庭,周末小亮和姐姐一起从家出发去图书馆借书,走了6分钟忘带借书证,小亮立即骑路边共享单车返回家中取借书证,姐姐以原来的速度继续向前行走,小亮取到借书证后骑单车原路原速前往图书馆,小亮追上姐姐后用单车带着姐姐一起前往图书馆.已知单车的速度是步行速度的3倍,如图是小亮和姐姐距家的路程y(米)与出发的时间x(分钟)的函数图象,根据图象解答下列问题:
⑴小亮在家停留了 分钟.
⑵求小亮骑单车从家出发去图书馆时距家的路程y(米)与出发时间x(分钟)之间的函数关系式.
⑶若小亮和姐姐到图书馆的实际时间为m分钟,原计划步行到达图书馆的时间为n分钟,则n-m= 分钟.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com