
分析 利用因式分解法求出方程2x2+3x+1=0的两根,由此即可得出点P的坐标,再根据点P与点Q关于原点对称,即可得出点Q的坐标.
解答 解:∵2x2+3x+1=(2x+1)(x+1)=0,
∴$\left\{\begin{array}{l}{a=-1}\\{b=-\frac{1}{2}}\end{array}\right.$或$\left\{\begin{array}{l}{a=-\frac{1}{2}}\\{b=-1}\end{array}\right.$,
∴点P的坐标为(-1,-$\frac{1}{2}$)或(-$\frac{1}{2}$,-1).
∵点P(a,b)关于原点对称的点Q,
∴点Q的坐标为(1,$\frac{1}{2}$)或($\frac{1}{2}$,1).
故答案为:(1,$\frac{1}{2}$)或($\frac{1}{2}$,1).
点评 本题考查了因式分解法解一元二次方程以及关于原点对称的点的坐标,利用因式分解法解方程求出点P的坐标是解题的关键.


 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案科目:初中数学 来源: 题型:填空题
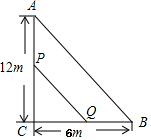 如图,在Rt△ABC中,∠C=90°,点P、Q同时由C、B两点出发,点P在CA上沿CA方向以2cm/s的速度移动,点Q在BC上沿BC方向以1cm/s的速度移动,则2或4秒钟后,△PCQ的面积为8cm2?
如图,在Rt△ABC中,∠C=90°,点P、Q同时由C、B两点出发,点P在CA上沿CA方向以2cm/s的速度移动,点Q在BC上沿BC方向以1cm/s的速度移动,则2或4秒钟后,△PCQ的面积为8cm2?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com