
【题目】已知:二次函数![]() ,当
,当![]() 时,函数有最大值5.
时,函数有最大值5.
(1)求此二次函数图象与坐标轴的交点;
(2)将函数![]() 图象x轴下方部分沿x轴向上翻折,得到的新图象与直线
图象x轴下方部分沿x轴向上翻折,得到的新图象与直线![]() 恒有四个交点,从左到右,四个交点依次记为
恒有四个交点,从左到右,四个交点依次记为![]() ,当以
,当以![]() 为直径的圆与
为直径的圆与![]() 轴相切时,求
轴相切时,求![]() 的值.
的值.
(3)若点![]() 是(2)中翻折得到的抛物线弧部分上任意一点,若关于m的一元二次方程
是(2)中翻折得到的抛物线弧部分上任意一点,若关于m的一元二次方程![]() 恒有实数根时,求实数k的最大值.
恒有实数根时,求实数k的最大值.
【答案】(1) 抛物线与![]() 轴交于
轴交于![]() ;(2)
;(2)![]() ;(3)实数k的最大值为3.
;(3)实数k的最大值为3.
【解析】分析:(1)求出对称轴x=1,结合a>0,可知当![]() 时,
时,![]() 随
随![]() 增大而增大,所以x=4时,y=5,把以x=4时,y=5代入解析式求出a的值,然后解方程
增大而增大,所以x=4时,y=5,把以x=4时,y=5代入解析式求出a的值,然后解方程![]() 即可;
即可;
(2)由折叠部分对应的解析式:![]() ,可知
,可知![]() ,解方程
,解方程![]() ,求出B、C的坐标,然后根据
,求出B、C的坐标,然后根据![]() 列方程即可求出n的值;
列方程即可求出n的值;
(3)根据△≥0求出k的取值范围,即![]() ,再结合
,再结合![]() ,即可求得实数k的最大值.
,即可求得实数k的最大值.
详解:(1) 抛物线![]() 的对称轴为:
的对称轴为:![]() .
.
![]()
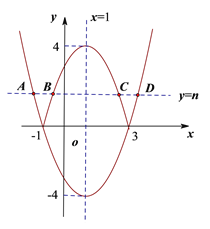
![]() ,抛物线开口向上,大致图象如图所示.
,抛物线开口向上,大致图象如图所示.
![]() 当
当![]() 时,
时,![]() 随
随![]() 增大而增大;
增大而增大;
由已知:当![]() 时,函数有最大值5.
时,函数有最大值5.
![]() 当
当![]() 时,
时, 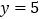 ,
,
![]() .
.
![]()
令![]() 得
得![]() ,令
,令![]() 得
得![]() ,
,
![]() 抛物线与
抛物线与![]() 轴交于
轴交于![]() ,
,
抛物线与![]() 轴交于
轴交于![]() .
.
(2)![]() ,
,
其折叠得到的部分对应的解析式为:![]() ,其顶点为
,其顶点为![]()
![]() 图象与直线
图象与直线![]() 恒有四个交点,
恒有四个交点,
![]()
![]()
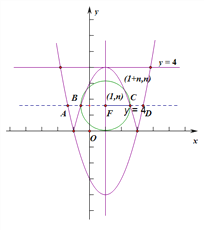
由![]() ,解得
,解得![]() ,
,
![]() ,
,![]() .
.
当以![]() 为直径的圆与
为直径的圆与![]() 轴相切时,
轴相切时,![]() .
.
即:![]() ,
,
![]() ,
,
![]() ,
,
得![]() ,
,![]()
![]() ,
,
![]()
![]() .
.
(另法:∵BC直径,且⊙F与x轴相切,
∴FC=y=n,
∵对称轴为直线x=1,
∴F(1,n),则C(1+n,n),
又∵C在![]() 上,
上,
∴![]() ,
,
得![]() ,
,
![]()
![]() ,
,
![]()
![]() .
.
(3)若关于m的一元二次方程![]() 恒有实数根,则须
恒有实数根,则须
![]() 恒成立,
恒成立,
即![]() 恒成立,即
恒成立,即![]() 恒成立.
恒成立.
![]() 点
点![]() 是(2)中翻折得到的抛物线弧部分上任意一点,
是(2)中翻折得到的抛物线弧部分上任意一点,
![]() ,
,
![]()
![]() ,(
,( ![]() 取
取 ![]() 值之下限)
值之下限)
![]() 实数k的最大值为3.
实数k的最大值为3.


科目:初中数学 来源: 题型:
【题目】如图,反比例函数![]() (
(![]() ,
, ![]() )的图象与直线
)的图象与直线![]() 相交于点C,过直线上点A(1,3)作AB⊥x轴于点B,交反比例函数图象于点D,且AB=3BD.
相交于点C,过直线上点A(1,3)作AB⊥x轴于点B,交反比例函数图象于点D,且AB=3BD.
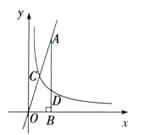
(1)求k的值;
(2)求点C的坐标;
(3)在y轴上确实一点M,使点M到C、D两点距离之和d=MC+MD,求点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
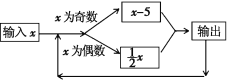
【题目】按如图所示的程序计算,如果开始输入的x的值为48,我们发现第一次输出得到的结果为24,第二次输出的结果为12,第三次得到的输出结果为6,……,则第2019次得到的结果为__.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】同学们都知道,![]() 表示4与-2的差的绝对值,实际上也可理解为4与-2两数在数轴上所对应的两点之间的距离,同理
表示4与-2的差的绝对值,实际上也可理解为4与-2两数在数轴上所对应的两点之间的距离,同理![]() 也可理解为
也可理解为![]() 与3两数在数轴上所对应的两点之间的距离,
与3两数在数轴上所对应的两点之间的距离,![]() 就表示
就表示![]() 在数轴上对应的点到-1的距离,由上面绝对值的几何意义,解答下列问题:
在数轴上对应的点到-1的距离,由上面绝对值的几何意义,解答下列问题:
(1)求![]() .
.
(2)若![]() ,则
,则![]() .
.
(3)请你找出所有符合条件的整数![]() ,使得
,使得![]() .
.
(4)求![]() 的最小值,并写出此时
的最小值,并写出此时![]() 的取值情况.
的取值情况.
(5)已知![]() ,求
,求![]() 的最大值和最小值.
的最大值和最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知数轴上三点A,O,B表示的数分别为6,0,-4,动点P从A出发,以每秒6个单位的速度沿数轴向左匀速运动.
(1)当点P到点A的距离与点P到点B的距离相等时,点P在数轴上表示的数是 ;
(2)另一动点R从B出发,以每秒4个单位的速度沿数轴向左匀速运动,若点P、R同时出发,问点P运动多少时间追上点R?
(3)若M为AP的中点,N为PB的中点,点P在运动过程中,线段MN的长度是否发生变化?若发生变化,请你说明理由;若不变,请你画出图形,并求出线段MN的长度.
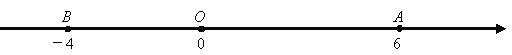
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]() (m是常数)的顶点为P,直线l:y=x﹣1
(m是常数)的顶点为P,直线l:y=x﹣1
(1)求证:点P在直线l上;
(2)当m=﹣3时,抛物线与x轴交于A,B两点,与y轴交于点C,与直线l的另一个交点为Q,M是x轴下方抛物线上的一点,∠ACM=∠PAQ(如图),求点M的坐标;
(3)若以抛物线和直线l的两个交点及坐标原点为顶点的三角形是等腰三角形,请直接写出所有符合条件的m的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某项工程如果由乙单独完成比甲单独完成多用6天;如果甲、乙先合做4天后,再由乙单独完成,那么乙一共所用的天数刚好和甲单独完成工程所用的天数相等.
(1)求甲单独完成全部工程所用的时间;
(2)该工程规定须在20天内完成,若甲队每天的工程费用是4.5万元,乙队每天的工程费用是2.5万元,请你选择上述一种施工方案,既能按时完工,又能使工程费用最少,并说明理由?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】类似于运算符号“![]() ”,新定义一种运算符号“⊙”,观察下列运算:
”,新定义一种运算符号“⊙”,观察下列运算:
1⊙3=1×5 +3 =8;
3⊙(-1)= 3×5+(-1)=14;
(-3)⊙4=(-3)×5+4=-11
(-5)⊙(-4)=(-5)×5+(-4)=-29 ;
(1) 归纳:用代数式表示a⊙b的结果为: ;
(2) 若2x⊙![]() =16,求
=16,求![]() 的值;
的值;
(3) 若a⊙![]() = 4,请计算
= 4,请计算![]() ⊙
⊙![]() 的值;
的值;
(4) 比较 ![]() ⊙
⊙![]() 与
与![]() ⊙(
⊙(![]() )的大小,并说理由.
)的大小,并说理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com