
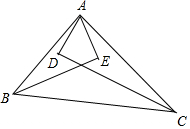
 如图,已知BE,CD是△ABC的角平分线,并且AE⊥BE于点E,AD⊥DC于点D,求证:
如图,已知BE,CD是△ABC的角平分线,并且AE⊥BE于点E,AD⊥DC于点D,求证:分析 (1)延长AD交BC于G,延长AE交BC于H,根据等腰三角形的三线合一得到AE=EH,BA=BH,得到DE是△AGH的中位线,根据三角形中位线定理证明;
(2)根据三角形中位线定理证明即可.
解答 证明:(1)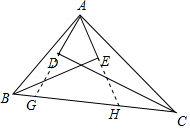 延长AD交BC于G,延长AE交BC于H,
延长AD交BC于G,延长AE交BC于H,
∵BE是△ABC的角平分线,BE⊥AH,
∴AE=EH,BA=BH,
同理,AD=DG,CA=CG,
∴DE是△AGH的中位线,
∴DE∥BC;
(2)∵DE是△AGH的中位线,
∴DE=$\frac{1}{2}$GH,
∵BA=BH,CA=CG,
∴GH=AB+AC-BC,
∴DE=$\frac{1}{2}$(AB+AC-BC).
点评 本题考查的是三角形的中位线定理,掌握三角形的中位线平行于第三边,且等于第三边的一半是解题的关键.


 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案科目:初中数学 来源: 题型:选择题
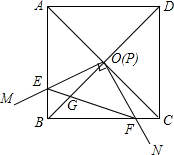 如图,边长为1的正方形ABCD的对角线AC,BD相交于点O,有直角∠MPN,使直角顶点P与点O重合,直角边PM,PN分别与OA,OB重合,然后逆时针旋转∠MPN,旋转角为α(0°<α<90°),PM,PN分别交AB,BC于E,F两点,连接EF交OB于点G,下列结论中错误的是( )
如图,边长为1的正方形ABCD的对角线AC,BD相交于点O,有直角∠MPN,使直角顶点P与点O重合,直角边PM,PN分别与OA,OB重合,然后逆时针旋转∠MPN,旋转角为α(0°<α<90°),PM,PN分别交AB,BC于E,F两点,连接EF交OB于点G,下列结论中错误的是( )| A. | OF=OE | |
| B. | BE+BF=$\sqrt{2}$OA | |
| C. | 在旋转的过程中,当△BEF与△COF的面积之和最大时,AE=$\frac{3}{4}$ | |
| D. | AE•BE=BO•BG. |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 为整治城市街道的汽车超速现象,交警大队在某街道旁进行了流动测速.如图,一辆小汽车在某城市街道上直行,某一时刻刚好行驶到离车速检测仪A60m的C处,过了4s后,小汽车到达离车速检测仪A100m的B处,已知该段城市街道的限速为60km/h,请问这辆小汽车是否超速?
为整治城市街道的汽车超速现象,交警大队在某街道旁进行了流动测速.如图,一辆小汽车在某城市街道上直行,某一时刻刚好行驶到离车速检测仪A60m的C处,过了4s后,小汽车到达离车速检测仪A100m的B处,已知该段城市街道的限速为60km/h,请问这辆小汽车是否超速?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com