
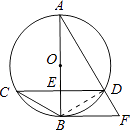
【题目】如图,已知⊙O的直径AB与弦CD互相垂直,垂足为点E.⊙O的切线BF与弦AD的延长线相交于点F,且AD=3,cos∠BCD= ![]() .
. 
(1)求证:CD∥BF;
(2)求⊙O的半径;
(3)求弦CD的长.
【答案】
(1)证明:∵BF是⊙O的切线,
∴AB⊥BF,
∵AB⊥CD,
∴CD∥BF
(2)解:连接BD,∵AB是直径,
∴∠ADB=90°,
∵∠BCD=∠BAD,cos∠BCD= ![]() ,
,
∴cos∠BAD= ![]() ,
,
又∵AD=3,
∴AB=4,
∴⊙O的半径为2
(3)解:∵∠BCD=∠DAE,
∴cos∠BCD=cos∠DAE= ![]() ,AD=3,
,AD=3,
∴AE=ADcos∠DAE=3× ![]() =
= ![]() ,
,
∴ED= ![]() ,
,
∴CD=2ED= ![]() .
.
【解析】(1)由BF是⊙O的切线得到AB⊥BF,而AB⊥CD,由此即可证明CD∥BF;(2)连接BD,由AB是直径得到∠ADB=90°,而∠BCD=∠BAD,cos∠BCD= ![]() ,所以cos∠BAD=
,所以cos∠BAD= ![]() ,然后利用三角函数即可求出⊙O的半径;(3)由于cos∠DAE=
,然后利用三角函数即可求出⊙O的半径;(3)由于cos∠DAE= ![]() ,而AD=3,由此求出AE,接着利用勾股定理可以求出ED,也就求出了CD.
,而AD=3,由此求出AE,接着利用勾股定理可以求出ED,也就求出了CD.


科目:初中数学 来源: 题型:
【题目】为进一步建设秀美、宜居的生态环境,某村欲购买甲、乙、丙三种树美化村庄,已知甲、乙丙三种树的价格之比为2:2:3,甲种树每棵200元,现计划用210000元资金,购买这三种树共1000棵.
(1)求乙、丙两种树每棵各多少元?
(2)若购买甲种树的棵树是乙种树的2倍,恰好用完计划资金,求这三种树各能购买多少棵?
(3)若又增加了10120元的购树款,在购买总棵树不变的前提下,求丙种树最多可以购买多少棵?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2018年俄罗斯世界杯组委会对世界杯比赛用球进行抽查,随机抽取了100个足球,检测每个足球的质量是否符合标准,超过或不足部分分别用正、负数来表示,记录如表:
与标准质量的差值(单位:克) | ﹣4 | ﹣2 | 0 | 1 | 3 | 6 |
个数 | 10 | 13 | 30 | 25 | 15 | 7 |
(1)平均每个足球的质量比标准质量多还是少?用你学过的方法合理解释;
(2)若每个足球标准质量为420克,则抽样检测的足球的总质量是多少克?
查看答案和解析>>
科目:初中数学 来源: 题型:
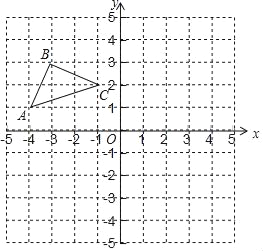
【题目】如图,在平面直角坐标系中,点O为坐标原点,已知△ABC三个定点坐标分别为A(﹣4,1),B(﹣3,3),C(﹣1,2).
(1)画出△ABC关于x轴对称的△A1B1C1,点A,B,C的对称点分别是点A1、B1、C1,直接写出点A1,B1,C1的坐标;
(2)画出点C关于y轴的对称点C2,连接C1C2,CC2,C1C,求△CC1C2的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题8分)如图,在五边形ABCDE中,∠BCD=∠EDC=90°,BC=ED,AC=AD.
(1)求证:△ABC≌△AED;
(2)当∠B=140°时,求∠BAE的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC=5,BC=6,E是BA延长线的一点,P是∠EAC的平分线上一个动点,当△APC是以AC为腰的等腰三角形时,△APC的面积为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】武汉市光谷实验中学九(1)班为了了解全班学生喜欢球类活动的情况,采取全面调查的方法,从足球、乒乓球、篮球、排球等四个方面调查了全班学生的兴趣爱好,根据调查的结果组建了4个兴趣小组,并绘制成如图所示的两幅不完整的统计图(如图①,②,要求每位学生只能选择一种自己喜欢的球类),下列说法错误的是( )

A. 九(1)班的学生人数为40 B. m的值为10
C. n的值为20 D. 表示“足球”的扇形的圆心角是70°
查看答案和解析>>
科目:初中数学 来源: 题型:
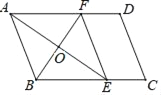
【题目】如图,在平行四边形ABCD中,∠BAD的平分线交BC于E,点F在AD上,且AF=AB,连接EF.
(1)判断四边形ABEF的形状并证明;
(2)若AE、BF相交于点O,且四边形ABEF的周长为20,BF=6,求AE的长度及四边形ABEF的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com