
| A. | 5≤S≤8 | B. | 5≤S≤9 | C. | 5≤S≤10 | D. | S≤5或S≥8 |
分析 根据反比例函数 y=$\frac{k}{x}$中k的几何意义,即图象上的点与原点所连的线段、坐标轴、向坐标轴作垂线所围成的直角三角形面积S的关系即S=$\frac{1}{2}$|k|.
解答 解:根据题意可得:∵A(2,5),B(8,2)两点,反比例函数y=$\frac{k}{x}$与线段MN相交,
∴k的范围是10≤k≤16;
∵△OGP面积S为$\frac{1}{2}$|k|;
∴△OGP面积S的取值范围是5≤S≤8.
故选A.
点评 本题主要考查了反比例函数 y=$\frac{k}{x}$中k的几何意义,即图象上的点与原点所连的线段、坐标轴、向坐标轴作垂线所围成的直角三角形面积S的关系即S=$\frac{1}{2}$|k|,是经常考查的一个知识点;这里体现了数形结合的思想,做此类题一定要正确理解k的几何意义.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
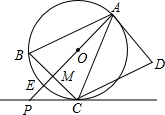 如图,AD是⊙O的切线,切点为A,AB是⊙O的弦,过点B作BC∥AD,交⊙O于点C,连接AC,过点C作CD∥AB,交AD于点D,连接AO并延长AO交BC于点M,交$\widehat{BC}$于点E,交过点C的直线于点P,且∠BCP=∠ACD.
如图,AD是⊙O的切线,切点为A,AB是⊙O的弦,过点B作BC∥AD,交⊙O于点C,连接AC,过点C作CD∥AB,交AD于点D,连接AO并延长AO交BC于点M,交$\widehat{BC}$于点E,交过点C的直线于点P,且∠BCP=∠ACD.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -4是16的平方根 | B. | 17是(-17)2的算术平方根 | ||
| C. | $\frac{1}{64}$的算术平方根是$\frac{1}{8}$ | D. | 0.9的算术平方根0.03 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com