
分析 由a+$\frac{1}{a}$=3根据a2+$\frac{1}{{a}^{2}}$=(a+$\frac{1}{a}$)2-2、a3+$\frac{1}{{a}^{3}}$=(a+$\frac{1}{a}$)(a2-1+$\frac{1}{{a}^{2}}$)、a4+$\frac{1}{{a}^{4}}$=(a2+$\frac{1}{{a}^{2}}$)2-2分别求出a2+$\frac{1}{{a}^{2}}$、a3+$\frac{1}{{a}^{3}}$、a4+$\frac{1}{{a}^{4}}$的值,继而可得答案.
解答 解:∵a+$\frac{1}{a}$=3,
∴(a+$\frac{1}{a}$)2=9,即a2+2+$\frac{1}{{a}^{2}}$=9,
∴a2+$\frac{1}{{a}^{2}}$=7,
则a3+$\frac{1}{{a}^{3}}$=(a+$\frac{1}{a}$)(a2-1+$\frac{1}{{a}^{2}}$)=3×(7-1)=18,
a4+$\frac{1}{{a}^{4}}$=(a2+$\frac{1}{{a}^{2}}$)2-2=79,
∴原式=7+18+79=104,
故答案为:104.
点评 本题主要考查分式的求值,熟练掌握完全平方公式和立方和公式是解题的关键.


 口算题天天练系列答案
口算题天天练系列答案科目:初中数学 来源: 题型:解答题
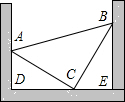 如图,把一块等腰直角三角形零件(△ABC,其中∠ACB=90°),放置在一凹槽内,三个顶点A,B,C分别落在凹槽内壁上,已知∠ADE=∠BED=90°,测得AD=5cm,BE=7cm,求该三角形零件的面积.
如图,把一块等腰直角三角形零件(△ABC,其中∠ACB=90°),放置在一凹槽内,三个顶点A,B,C分别落在凹槽内壁上,已知∠ADE=∠BED=90°,测得AD=5cm,BE=7cm,求该三角形零件的面积.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,正方形ABCD,以AB为腰向外作等腰△ABE,连接DE交AB于点F,∠BAE的平分线交EF于点G,过D点作AG的垂线交GA的延长线于点H,已知tan∠EDA=$\frac{3}{4}$,S△AEF=9,则AH的长为$\frac{2\sqrt{21}}{7}$.
如图,正方形ABCD,以AB为腰向外作等腰△ABE,连接DE交AB于点F,∠BAE的平分线交EF于点G,过D点作AG的垂线交GA的延长线于点H,已知tan∠EDA=$\frac{3}{4}$,S△AEF=9,则AH的长为$\frac{2\sqrt{21}}{7}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在平面直角坐标系中,直线AB与y轴在正半轴、x轴正半轴分别交A、B两点,M在BA的延长线上,PA平分∠MAO,PB平分∠ABO,则∠P=45°.
如图,在平面直角坐标系中,直线AB与y轴在正半轴、x轴正半轴分别交A、B两点,M在BA的延长线上,PA平分∠MAO,PB平分∠ABO,则∠P=45°.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
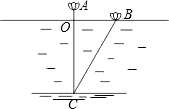 印度数学家什迦罗(1141年-1225年)曾提出过“荷花问题”:
印度数学家什迦罗(1141年-1225年)曾提出过“荷花问题”:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在△ABC中,D、E分别是边BC、AB上的点,BE=AE,BD=2CD,△AEC的面积为S1,△ADC的面积为S2,若△ABC的面积为8,则S1-S2=$\frac{4}{3}$.
如图,在△ABC中,D、E分别是边BC、AB上的点,BE=AE,BD=2CD,△AEC的面积为S1,△ADC的面积为S2,若△ABC的面积为8,则S1-S2=$\frac{4}{3}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com