
【题目】问题提出:
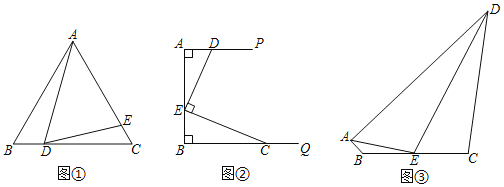
(1)如图①,在边长为8的等边三角形ABC中,点D,E分别在BC与AC上,且BD=2,∠ADE=60°,则线段CE的长为 .
问题
(2)如图②,已知AP∥BQ,∠A=∠B=90°,AB=6,D是射线AP上的一个动点(不与点A重合),E是线段AB上的一个动点(不与A,B重合),EC⊥DE,交射线BQ于点C,且AD+DE=AB,求△BCE的周长.
问题解决:
(3)如图③,在四边形ABCD中,AB+CD=10(AB<CD),BC=6,点E为BC的中点,且∠AED=108°,则边AD的长是否存在最大值?若存在,请求AD的最大值,并求出此时AB,CD的长度,若不存在,请说明理由.
【答案】(1)![]() ;(2)12;(3)存在,AD的最大值为
;(2)12;(3)存在,AD的最大值为![]() .
.
【解析】
问题提出(1)证明△ABD∽△DCE,得出![]() =
=![]() ,即可得出答案;
,即可得出答案;
问题分析(2)设AD=x,AE=y,则DE=6-x,BE=6-y,证明△ADE∽△BEC,得出![]() =
=![]() =
=![]() ,即
,即![]() =
=![]() =
=![]() ,求出BC,CE,得出△BCE的周长=
,求出BC,CE,得出△BCE的周长=![]() ,在Rt△ADE中,结合勾股定理可得出△BCE的周长;
,在Rt△ADE中,结合勾股定理可得出△BCE的周长;
问题解决(3)作出点B关于AE的对称点M,点C关于DE的对称点N,连接AM、EM,MN、DN、EN.证明△MNE是等腰三角形,EM=EN=3,得出∠EMN=∠ENM=![]() (180°-36°)=72°,作∠EMN的平分线交EN于P,证出PE=PM=MN,证明△MPN∽△EMN,得出
(180°-36°)=72°,作∠EMN的平分线交EN于P,证出PE=PM=MN,证明△MPN∽△EMN,得出![]() =
=![]() ,则MN2=EN×PN,设PE=PM=MN=x,则PN=3-x,得出x2=3(3-x),得出MN,由AD≤AM+MN+DN,即可得出答案.
,则MN2=EN×PN,设PE=PM=MN=x,则PN=3-x,得出x2=3(3-x),得出MN,由AD≤AM+MN+DN,即可得出答案.
问题提出:
(1)解:∵△ABC是等边三角形,
∴AB=BC=8,∠B=∠C=60°,
∵BD=2,
∴CD=BC﹣BD=6,
∵∠ADC=∠ADE+∠CDE=∠B+∠BAD,∠ADE=60°,
∴∠BAD=∠CDE,
∴△ABD∽△DCE,
∴![]() =
=![]() ,即
,即![]() =
=![]() ,
,
解得:CE=![]() ;
;
故答案为:![]() ;
;
问题
(2)解:∵AD+DE=AB,AB=6,
∴AD+DE=6,
设AD=x,AE=y,则DE=6﹣x,BE=6﹣y,
∵EC⊥DE,∴∠DEC=90°,∴∠AED+∠BEC=90°,
∵∠A=∠B=90°,∴∠AED+∠ADE=90°,∴∠ADE=∠BEC,
∴△ADE∽△BEC,∴![]() =
=![]() =
=![]() ,
,
即![]() =
=![]() =
=![]() ,
,
解得:BC=![]() ,CE=
,CE=![]() ,
,
∴△BCE的周长=BE+BC+CE=6﹣y+![]()
![]() =
=![]() ,
,
在Rt△ADE中,由勾股定理得:x2+y2=(6﹣x)2,
整理得:36﹣y2=12x,
∴△BCE的周长=![]() =12;
=12;
问题解决:
(3)解:作出点B关于AE的对称点M,点C关于DE的对称点N,连接AM、EM,MN,DN,EN.如图所示:
根据轴对称的性质可得AM=AB,BE=EM,CE=EN,DN=CD,∠AEB=AEM,∠DEC=∠DMN,
∵∠AED=108°,
∴∠AEB+∠DEC=180°﹣∠AED=180°﹣108°=72°,
∴∠MEN=∠AED﹣(∠AEM+∠DEN)=108°﹣72°=36°,
∵点M是四边形ABCD的边BC的中点,
∴BE=CE=3,
∴EM=EN=3,
∴∠EMN=∠ENM=![]() (180°﹣36°)=72°,
(180°﹣36°)=72°,
作∠EMN的平分线交EN于P,则∠EMP=∠NMP=36°=∠MEN,∠MPN=36°+36°=72°=∠ENM,
∴PE=PM=MN,△MPN∽△EMN,
∴![]() =
=![]() ,
,
∴MN2=EN×PN,
设PE=PM=MN=x,则PN=3﹣x,
∴x2=3(3﹣x),
解得:x=![]() ,或x=
,或x=![]() (舍去),
(舍去),
∴MN=![]() ,
,
∵AD≤AM+MN+DN=AB+CD+MN=10+![]() =
=![]() ,
,
∴AD≤![]() ,
,
∴AD的最大值为![]() .
.



科目:初中数学 来源: 题型:
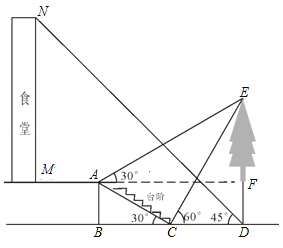
【题目】(2017湖北省鄂州市)小明想要测量学校食堂和食堂正前方一棵树的高度,他从食堂楼底M处出发,向前走3米到达A处,测得树顶端E的仰角为30°,他又继续走下台阶到达C处,测得树的顶端E的仰角是60°,再继续向前走到大树底D处,测得食堂楼顶N的仰角为45°.已知A点离地面的高度AB=2米,∠BCA=30°,且B、C、D三点在同一直线上.
(1)求树DE的高度;
(2)求食堂MN的高度.
查看答案和解析>>
科目:初中数学 来源: 题型:
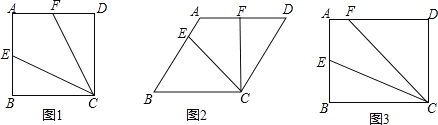
【题目】在四边形ABCD中,点E、F分别是AB、AD边上一点,∠DFC=2∠FCE.
(1)如图1,若四边形ABCD是正方形,∠DFC=60°,BE=4,则AF= .
(2)如图2,若四边形ABCD是菱形,∠A=120°,∠DFC=90°,BE=4,求![]() 的值.
的值.
(3)如图3,若四边形ABCD是矩形,点E是AB的中点,CE=12,CF=13,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
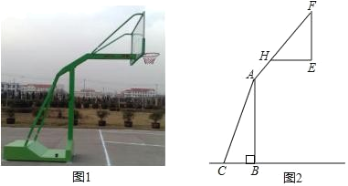
【题目】如图1,2分别是某款篮球架的实物图与示意图,已知底座BC的长为0.60m,底座BC与支架AC所成的角∠ACB=75°,点A、H、F在同一条直线上,支架AH段的长为1m,HF段的长为1.50m,篮板底部支架HE的长为0.75m.
(1)求篮板底部支架HE与支架AF所成的角∠FHE的度数.
(2)求篮板顶端F到地面的距离.(结果精确到0.1 m;参考数据:cos75°≈0.2588,sin75°≈0.9659,tan75°≈3.732,![]() ≈1.732,
≈1.732,![]() ≈1.414)
≈1.414)
查看答案和解析>>
科目:初中数学 来源: 题型:
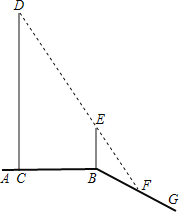
【题目】如图,平台AB上有一棵直立的大树CD,平台的边缘B处有一棵直立的小树BE,平台边缘B外有一个向下的斜坡BG.小明想利用数学课上学习的知识测量大树CD的高度.一天,他发现大树的影子一部分落在平台CB上,一部分落在斜坡上,而且大树的顶端D与小树顶端E的影子恰好重合,且都落在斜坡上的F处,经测量,CB长5![]() 米,BF长2米,小树BE高1.8米,斜坡BG与平台AB所成的∠ABG=150°.请你帮小明求出大树CD的高度.
米,BF长2米,小树BE高1.8米,斜坡BG与平台AB所成的∠ABG=150°.请你帮小明求出大树CD的高度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果一元二次方程ax2+bx+c=0 的两根 x1,x2均为正数,其中x1>x2,且满足1<x1﹣x2<2,那么称这个方程有“友好根”.
(1)方程(x﹣![]() )(x﹣
)(x﹣![]() )=0_____“友好根”(填:“有”或“没有”);
)=0_____“友好根”(填:“有”或“没有”);
(2)已知关于x的 x2﹣(t﹣1)x+t﹣2=0有“友好根”,求 t的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为弘扬传统文化,某校开展了“传承经典文化,阅读经典名著”活动.为了解七、八年级学生(七、八年级各有600名学生)的阅读效果,该校举行了经典文化知识竞赛.现从两个年级各随机抽取20名学生的竞赛成绩(百分制)进行分析,过程如下:
收集数据:
七年级:79,85,73,80,75,76,87,70,75,94,75,79,81,71,75,80,86,59,83,77.
八年级:92,74,87,82,72,81,94,83,77,83,80,81,71,81,72,77,82,80,70,41.
整理数据:
|
|
|
|
|
| |
七年级 | 0 | 1 | 0 | a | 7 | 1 |
八年级 | 1 | 0 | 0 | 7 | b | 2 |
分析数据:
平均数 | 众数 | 中位数 | |
七年级 | 78 | 75 |
|
八年级 | 78 |
| 80.5 |
应用数据:
(1)由上表填空:a= ,b= ,c= ,d= .
(2)估计该校七、八两个年级学生在本次竞赛中成绩在90分以上的共有多少人?
(3)你认为哪个年级的学生对经典文化知识掌握的总体水平较好,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=4,BC=2,点E是边BC的中点,P为AB上一点,连接PE,过点E作PE的垂线交射线AD于点Q,连接PQ,设AP的长为t.
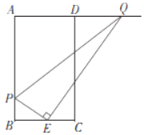
(1)用含t的代数式表示AQ的长;
(2)若△PEQ的面积等于10,求t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线y=ax2+bx+c的顶点坐标为(2,9),与y轴交于点A(0,5),与x轴交于点E,B.
(1)求二次函数y=ax2+bx+c的解析式;
(2)过点A作AC平行于x轴,交抛物线于点C,点P为抛物线上的一点(点P在AC上方),作PD平行于y轴交AB于点D,问当点P在何位置时,线段PD最长?并求出最大值;
(3)若点M在抛物线上,点N在其对称轴上,使得以A,E,N,M为顶点的四边形是平行四边形,求点M的坐标.(请直接写出结果)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com