
【题目】如图,甲、乙两座建筑物的水平距离BC为30m,从甲的顶部A处测得乙的顶部D处的俯角为35°测得底部C处的俯角为43°,求甲、乙两建筑物的高度AB和DC(结果取整数).
(参考数据:tan35°≈0.70,tan43°≈0.93)
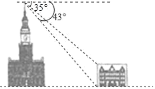
【答案】AB为28m,DC为7m.
【解析】
作AE⊥CD交CD的延长线于E.则四边形ABCE是矩形,根据矩形的性质可多AE=BC=30,AB=CE,在Rt△ACE中,由EC=AEtan43°求得EC的长,即可得AB的长;在Rt△AED中,DE=AEtan35°,由CD=EC﹣DE 即可求得CD的长.
如图作AE⊥CD交CD的延长线于E.则四边形ABCE是矩形,

∴AE=BC=30,AB=CE,
在Rt△ACE中,EC=AEtan43°≈27.9(m),
∴AB=CE≈27.9(m),
在Rt△AED中,DE=AEtan35°,
∴CD=EC﹣DE=AEtan43°﹣AEtan35°=30×0.93﹣30×0.7≈7(m),
答:甲、乙建筑物的高度AB为28m,DC为7m.


科目:初中数学 来源: 题型:
【题目】如图,圆O的直径为5,在圆O上位于直径AB的异侧有定点C和动点P,已知BC∶CA=4∶3,点P在半圆弧AB上运动(不与A、B重合),过C作CP的垂线CD交PB的延长线于D点
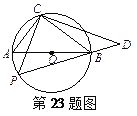
(1)求证:AC·CD=PC·BC;
(2)当点P运动到AB弧中点时,求CD的长;
(3)当点P运动到什么位置时,△PCD的面积最大?并求这个最大面积S.
查看答案和解析>>
科目:初中数学 来源: 题型:
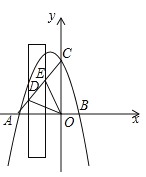
【题目】如图,抛物线![]() 与x轴交于点A,B(点A在点B的左侧),与y轴交于点C,连结AC,现有一宽度为1,且长与y轴平行的矩形沿x轴方向平移,交直线AC于点D和E,△ODE周长的最小值为( )
与x轴交于点A,B(点A在点B的左侧),与y轴交于点C,连结AC,现有一宽度为1,且长与y轴平行的矩形沿x轴方向平移,交直线AC于点D和E,△ODE周长的最小值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
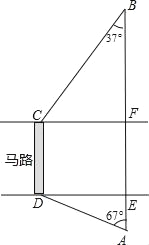
【题目】如图,马路的两边CF、DE互相平行,线段CD为人行横道,马路两侧的A、B两点分别表示车站和超市,CD与AB所在直线互相平行,且都与马路的两边垂直.马路宽20米,A,B相距62米,∠A=67°,∠B=37°.求CD与AB之间的距离.(参考数据:sin67°≈![]() ,cos67°≈
,cos67°≈![]() ,tan67°≈
,tan67°≈![]() ,sn37°≈
,sn37°≈![]() ,cos37°≈
,cos37°≈![]() ,tan37°≈
,tan37°≈![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将△ABC绕点C顺时针旋转90°得到△EDC.若点A,D,E在同一条直线上,∠ACB=20°,则∠ADC的度数是![]()
![]()

A. 55° B. 60° C. 65° D. 70°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程ax2+bx+c=0的两实数根为x1,x2,根据一元二次方程解的意义和因式分解法解一元二次方程可知,x1,x2也是(x﹣x1)(x﹣x2)=0的两个实数根,所以ax2+bx+c=a(x﹣x1)(x﹣x2).
利用这个结论可以解决一些相关问题.
(1)实数范围内因式分解:
例:分解因式2x2+2x﹣1
解:令2x2+2x﹣1=0,解这个方程,得
![]() =
=![]() .
.
即x1=![]() ,x2=
,x2=![]() .
.
所以 2x2+2x﹣1=![]() .
.
试仿照上例在实数范围内分解因式:x2﹣6x+1;
(2)解不等式:x2+2x﹣1>0;
(3)灵活运用:
已知方程(x﹣a)(x﹣b)﹣x=0的两个实数根是c、d,求方程(2x﹣c)(2x﹣d)+2x=0的根.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,![]() 为半圆的直径,点
为半圆的直径,点![]() 为圆心,
为圆心,![]() 为半圆的切线,过半圆上的点
为半圆的切线,过半圆上的点![]() 作
作![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() .
.
(1)连接![]() ,若
,若![]() ,求证:
,求证:![]() 是半圆的切线;
是半圆的切线;
(2)如图2,当线段![]() 与半圆交于点
与半圆交于点![]() 时,连接
时,连接![]() ,
,![]() ,判断
,判断![]() 和
和![]() 的数量关系,并证明你的结论.
的数量关系,并证明你的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】3月12日是我国义务植树节。某校组织学生开展义务植树活动,在活动结束后随机调查了40名学生每人植树的棵数,根据调查获取的样本数据,制作了不完整的扇形统计图和条形统计图.请根据相关信息,解答下列问题:

(Ⅰ)扇形统计图中m的值是_____________,补全条形统计图
(Ⅱ)求抽取的这部分学生植树棵数的平均数;
(Ⅲ)若本次活动共有320名学生参加,估计植树棵数超过8棵的约有多少人。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线 y ax2 bx c a 0经过点 A2, 0、 B 5, 0.
(1)用含 a 的代数式表示b 、c ;
(2)若点C 6, 4在抛物线上,在抛物线上找一点 P ,使 x 轴恰好平分CAP ,若存在求出点 P ,并求出此时ACP 的面积;
(3)在(2)的条件下,在抛物线的对称轴上是否存在一点Q,使tan AQC 2 ,若存在求出点Q 的坐标,若不存在请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com