
分析 (1)先求出b2-4ac的值,代入公式求出即可;
(2)先根据特殊角的三角函数值,负整数指数幂,有理数的乘方分别计算,最后求出即可.
解答 解:(1)2x2-9x+8=0
b2-4ac=(-9)2-4×2×8=17,
x=$\frac{9±\sqrt{17}}{2×2}$,
x1=$\frac{9+\sqrt{17}}{4}$,x2=$\frac{9-\sqrt{17}}{4}$;
(2)原式=2×$\frac{\sqrt{3}}{2}$-3×$\frac{\sqrt{3}}{3}$-$\frac{1}{2}$+(-1)
=$\sqrt{3}$-$\sqrt{3}$-$\frac{1}{2}$-1
=-1$\frac{1}{2}$.
点评 本题考查了解一元二次方程,特殊角的三角函数值,负整数指数幂,有理数的乘方的应用,能熟记知识点是解此题的关键,题目比较好,难度适中.


 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:初中数学 来源: 题型:选择题
| A. | 0°<α<30° | B. | 30°<α<45° | C. | 45°<α<60° | D. | 60°<α<90° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 如果两个角相等,那么它们是对顶角 | |
| B. | 如果a-b>0,那么a2-b2>0 | |
| C. | 两个锐角之和一定是钝角 | |
| D. | 两边及其夹角分别相等的两个三角形全等 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
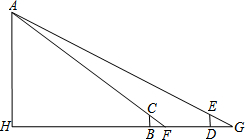 如图,要测量建筑物AH的高度,可以采用以下方法:立两根高2米长的标杆BC和DE,两杆之间的距离BD=20米,并使D,B,H三点在一条直线上;从点B处退行5米到点F处,人的眼睛贴着地面观察A点,使A,C,F三点成一线;从D处退行6米到点G处,从G观察A点,使A,E,G三点也成一线.请你利用以上的信息计算出AH的高度(测量过程中,建筑物AH,标杆BC和DH均与地面垂直).
如图,要测量建筑物AH的高度,可以采用以下方法:立两根高2米长的标杆BC和DE,两杆之间的距离BD=20米,并使D,B,H三点在一条直线上;从点B处退行5米到点F处,人的眼睛贴着地面观察A点,使A,C,F三点成一线;从D处退行6米到点G处,从G观察A点,使A,E,G三点也成一线.请你利用以上的信息计算出AH的高度(测量过程中,建筑物AH,标杆BC和DH均与地面垂直).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 阅读下面的材料:
阅读下面的材料:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com