
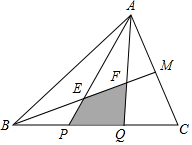
 如图,S△ABC=1,AM=MC,BP=PQ=QC,求阴影部分的面积.
如图,S△ABC=1,AM=MC,BP=PQ=QC,求阴影部分的面积. 分析 S△ABC=1、AM=MC、BP=PQ=QC知S△ABM=S△BCM=$\frac{1}{2}$S△ABC=$\frac{1}{2}$、S△APQ=S△ABP=S△AQC=$\frac{1}{3}$S△ABC=$\frac{1}{3}$,连接QM,知QM为△ACP的中位线,则AP=2MQ,MQ∥AP,从而得BE=EM、MQ=2EP,设BE=a,EP=b,则EM=a、MQ=2b、AP=4b,由AE∥MQ知$\frac{EF}{MF}=\frac{AE}{QM}$=$\frac{3b}{2b}=\frac{3}{2}$,从而得出EF=$\frac{3}{5}$a、FG=$\frac{2}{5}a$,则BE:EF:FG=a:$\frac{3}{5}$a:$\frac{2}{5}$a=5:3:2,继而得出S△AEF=$\frac{3}{10}$S△ABM=$\frac{3}{10}$×$\frac{1}{2}$=$\frac{3}{20}$,根据S阴影=S△APQ-S△AEF可得答案.
解答 解:∵S△ABC=1,AM=MC,BP=PQ=QC,
∴S△ABM=S△BCM=$\frac{1}{2}$S△ABC=$\frac{1}{2}$,
S△APQ=S△ABP=S△AQC=$\frac{1}{3}$S△ABC=$\frac{1}{3}$,
连接QM,
∵PQ=QC,AM=CM,
∴QM为△ACP的中位线,
则AP=2MQ,MQ∥AP.
∵EP∥MQ,
∴$\frac{BE}{EM}=\frac{BP}{PQ}$=1,$\frac{EP}{MQ}=\frac{BP}{BQ}=\frac{1}{2}$,即BE=EM,MQ=2EP,
设BE=a,EP=b,
则EM=a,MQ=2b,AP=4b,
∴AE=3b,
∵AE∥MQ,
∴$\frac{EF}{MF}=\frac{AE}{QM}$=$\frac{3b}{2b}=\frac{3}{2}$,
∴EF=$\frac{3}{5}$a,FG=$\frac{2}{5}a$,
∴BE:EF:FG=a:$\frac{3}{5}$a:$\frac{2}{5}$a=5:3:2,
∴S△AEF=$\frac{3}{10}$S△ABM=$\frac{3}{10}$×$\frac{1}{2}$=$\frac{3}{20}$,
则S阴影=S△APQ-S△AEF=$\frac{1}{3}$-$\frac{3}{20}$=$\frac{11}{60}$.
点评 本题主要考查三角形的面积即平行线分线段成比例定理,熟练掌握等底共高时三角形面积间的关系及平行线分线段成比例定理是解题的关键.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 将一列整数1,2,3,-4,-5,-6,7,-8,-9,-10,…按如图所示排列.如第一个顶峰的数是-6,第二个峰顶的数是15,那么第2016个峰顶的数是( )
将一列整数1,2,3,-4,-5,-6,7,-8,-9,-10,…按如图所示排列.如第一个顶峰的数是-6,第二个峰顶的数是15,那么第2016个峰顶的数是( )| A. | 18150 | B. | -18150 | C. | 18141 | D. | -18141 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{a+b}{2}$ | B. | $\frac{a+b}{11}$ | C. | $\frac{5a+6b}{11}$ | D. | $\frac{1}{2}$($\frac{a}{5}$+$\frac{b}{6}$) |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com