
分析 (1)把A(3,1)y=$\frac{k}{x}$ 即可得到结论;
(2)解$\left\{\begin{array}{l}{y=\frac{3}{x}}\\{y=ax+6}\end{array}\right.$得ax2+6x-3=0,根据题意得到△=36+12a=0,解方程即可得到结论.
解答 解:(1)∵反比例函数y=$\frac{k}{x}$ 的图象过点A(3,1),
∴k=3,
∴反比例函数的解析式为:y=$\frac{3}{x}$;
(2)解$\left\{\begin{array}{l}{y=\frac{3}{x}}\\{y=ax+6}\end{array}\right.$得ax2+6x-3=0,
∵一次函数y=ax+6(a≠0)的图象与反比例函数的图象只有一个交点,
∴△=36+12a=0,
∴a=-3,
∴一次函数的解析式为y=-3x+6.
点评 本题考查了一次函数与反比例函数的交点问题,待定系数法求函数的解析式,一元二次方程根的判别式,正确的理解题意是解题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
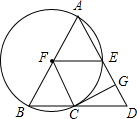 如图,在△ABD中,AB=AD,以AB为直径的⊙F交BD于点C,交AD于点E,CG⊥AD于点G,连接FE,FC.
如图,在△ABD中,AB=AD,以AB为直径的⊙F交BD于点C,交AD于点E,CG⊥AD于点G,连接FE,FC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 售价x(元/千克) | … | 50 | 60 | 70 | 80 | … |
| 销售量y(千克) | … | 100 | 90 | 80 | 70 | … |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
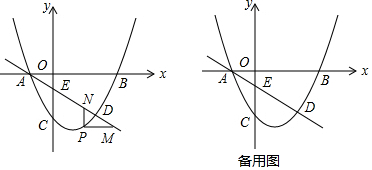
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某公司共有A、B、C三个部门,根据每个部门的员工人数和相应每人所创的年利润绘制成如下的统计表和扇形图
某公司共有A、B、C三个部门,根据每个部门的员工人数和相应每人所创的年利润绘制成如下的统计表和扇形图| 部门 | 员工人数 | 每人所创的年利润/万元 |
| A | 5 | 10 |
| B | b | 8 |
| C | c | 5 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com