
【题目】在△ABC与△CDE中,∠ACB![]() ∠CDE
∠CDE![]() 90°,AC
90°,AC![]() BC,CD
BC,CD![]() ED,连接AE,BE,F为AE的中点,连接DF,△CDE绕着点C旋转.
ED,连接AE,BE,F为AE的中点,连接DF,△CDE绕着点C旋转.
(1)如图1,当点D落在AC上时,DF与BE的数量关系是: ;
(2)如图2,当△CDE旋转到该位置时,DF与BE是否仍具有(1)中的数量关系,如果具有,请给予证明;如果没有,请说明理由;
(3)如图3,当点E落在线段CB延长线上时,若CD![]() AC
AC![]() 2,求DF的长.
2,求DF的长.
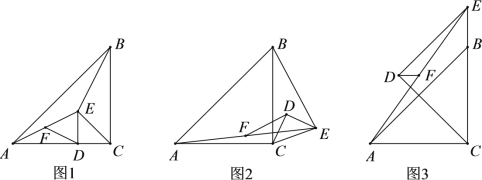
【答案】(1)DF=![]() BE;(2)见解析;(3)
BE;(2)见解析;(3)![]() ;
;
【解析】
(1)证明△ACE≌△BCE,则AE=BE,DF是直角△ADE的中线,DF=![]() AE,即可证明DF=
AE,即可证明DF=![]() BE;
BE;
(2)连接AM,证明△ACM≌△BCE,则AM=BE,DF为△AME的中位线,DF=![]() =
=![]() BE;
BE;
(3)易知CD=DE=2,由勾股定理CE=![]() ,BE=CE—CB=
,BE=CE—CB=![]() ,DF=
,DF=![]() BE,可求得DF=
BE,可求得DF=![]() .
.
(1) ∵∠ACB=∠CDE=90°,AC=BC,CD =ED,
∴∠ACE=∠BCE=45°,
∴△ACE≌△BCE,
∴AE=BE,因为DF是直角△ADE的中线,
∴DF=![]() AE
AE
∴DF=![]() BE
BE
(2)如图,将△CDE沿着CD翻折,得到△DCM≌△DCE,连接AM,

由△CDE为等腰直角三角形易知△CME为等腰直角三角形,
在△ACM和△BCE中,
AC=BC,∠ACM=∠BCE ,CM=CE,
∴△ACM≌△BCE,
∴AM=BE
∵F为AE的中点,D为ME的中点
∴DF为△AME的中位线,
∴DF=![]() ,
,
∴DF=![]() BE.
BE.
(3)将△EDC沿DC翻折得到△DCM
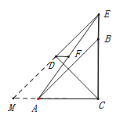
CD=DE=2,由勾股定理可知CE=![]()
BE=CE—CB=![]()
由前面的结论可知:DF=![]() BE
BE
∴DF=![]() .
.


科目:初中数学 来源: 题型:
【题目】为了维护国家主权和海洋权利,我国海监部门对中国海域实现常态化管理.某日,我国海监船在某海岛附近的海域执行巡逻任务.如图,此时海监船位于海岛P的北偏东30°方向,距离海岛100海里的A处,它沿正南方向航行一段时间后,到达位于海岛P的南偏东45°方向的B处,求海监船航行了多少海里(结果保留根号)?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正△ABC的边长为2,以BC边上的高AB1为边作正△AB1C1,△ABC与△AB1C1公共部分的面积记为S1;再以正△AB1C1边B1C1上的高AB2为边作正△AB2C2,△AB1C1与△AB2C2公共部分的面积记为S2;…,以此类推,则Sn=____.(用含n的式子表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】分已知关于x的一元二次方程(m-2)x2+(2m+1)x+m=0有两个实数根x1,x2.
(1)求m的取值范围.
(2)若|x1|=|x2|,求m的值及方程的根.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知点A(-1.5,0),B(0,2),将△ABO顺着x轴的正半轴无滑动的滚动,第一次滚动到①的位置,点B的对应点记作B1;第二次滚动到②的位置,点B1的对应点记作B2;第三次滚动到③的位置,点B2的对应点记作B3;![]() ;依次进行下去,则点B2020的坐标为__________.
;依次进行下去,则点B2020的坐标为__________.
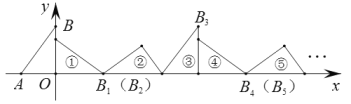
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校初二对某班最近一次数学测验或续(得分取整数)进行统计分析,将所有成绩由低到高分成五组,并绘制成如图所示的频数分布直方图,请结合直方图提供的信息,回答下列问题:
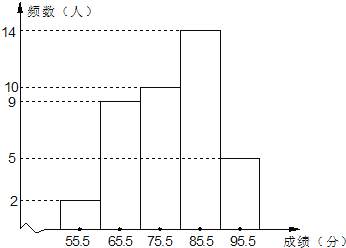
(1)该班共有名同学参加这次测验;
(2)这次测验成绩的中位数落在第几组内(从左到右数);
(3)若该校一共有360名初二学生参加这次测验,成绩80分以上(不含80分)为优秀,估计该校这次数学测验的优秀人数是多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,E是BC延长线上一点,在AB上取一点F,使点B关于直线EF的对称点G落在AD上,连接EG交CD于点H,连接BH交EF于点M,连接CM.则下列结论,其中正确的是( )
①∠1=∠2;
②∠3=∠4;
③GD=![]() CM;
CM;
④若AG=1,GD=2,则BM=![]() .
.
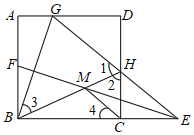
A.①②③④B.①②C.③④D.①②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,点A在x轴上,OA=4,将OA绕点O逆时针旋转120°至OB的位置.
(1)求经过A、O、B三点的抛物线的函数解析式;
(2)在此抛物线的对称轴上是否存在点P使得以P、O、B三点为顶点的三角形是等腰三角形?若存在,求出点P的坐标;若不存在,请说明理由;
(3 )如图2,OC=4,⊙A的半径为2,点M是⊙A上的一个动点,求MC+![]() OM的最小值.
OM的最小值.
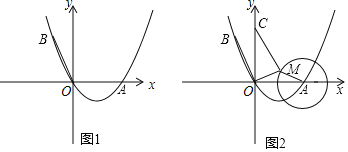
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com