
����Ŀ����ͼ������ABCD�ı߳�Ϊ2cm����DAB=60�㣮��P��A��������� ![]() cm/s���ٶȣ���AC��C�������˶������ͬʱ����QҲ��A���������1cm/s���ٶȣ�������AB�������˶�����P�˶���C��ʱ��P��Q��ֹͣ�˶������P�˶���ʱ��Ϊts��
cm/s���ٶȣ���AC��C�������˶������ͬʱ����QҲ��A���������1cm/s���ٶȣ�������AB�������˶�����P�˶���C��ʱ��P��Q��ֹͣ�˶������P�˶���ʱ��Ϊts�� 
��1����P����A��Cʱ����˵��PQ��BC��
��2����PΪԲ�ġ�PQ��Ϊ�뾶��Բ�����ʣ��������˶������У�tΪ������ֵʱ����P���BC�ֱ���1���������2�������㣿
���𰸡�
��1���⣺���ı���ABCD�����Σ�������ABCD�ı߳�Ϊ2cm��
��AB=BC=2����BAC= ![]() ��DAB��
��DAB��
�֡ߡ�DAB=60�㣨��֪����
���BAC=��BCA=30�㣻
��ͼ1������BD��AC��O��
���ı���ABCD�����Σ�
��AC��BD��OA= ![]() AC��
AC��
��OB= ![]() AB=1��30������Ե�ֱ�DZ���б�ߵ�һ�룩��
AB=1��30������Ե�ֱ�DZ���б�ߵ�һ�룩��
��OA= ![]() ��cm����AC=2OA=2
��cm����AC=2OA=2 ![]() ��cm����
��cm����
�˶�ts�� ![]() ��
��
�� ![]()
�֡ߡ�PAQ=��CAB��
���PAQ�ס�CAB��
���APQ=��ACB�����������εĶ�Ӧ����ȣ���
��PQ��BC��ͬλ����ȣ���ֱ��ƽ�У�
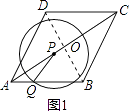
��2���⣺��ͼ2����P��BC���ڵ�M������PM����PM��BC��
��Rt��CPM�У��ߡ�PCM=30�㣬��PM= ![]() PC=
PC= ![]()
��PM=PQ=AQ=t���� ![]() =t
=t
���t=4 ![]() ��6����ʱ��P���BC��һ�������㣻
��6����ʱ��P���BC��һ�������㣻
��ͼ3����P����B����ʱPQ=PB��
�ߡ�PQB=��PAQ+��APQ=60��
���PQBΪ�ȱ������Σ���QB=PQ=AQ=t����t=1
�� ![]() ʱ����P���BC��2�������㣮
ʱ����P���BC��2�������㣮
��ͼ4����P����C����ʱPC=PQ����2 ![]() -
- ![]() t=t����t=3��
t=t����t=3�� ![]() ��
��
�൱1��t��3�� ![]() ʱ����P���BC��һ�������㣬
ʱ����P���BC��һ�������㣬
����P�˶�����C����t=2ʱP��C�غϣ�Q��B�غϣ�Ҳֻ��һ�����㣬��ʱ����P���BC��һ�������㣬
�൱t=4 ![]() ��6��1��t��3��
��6��1��t��3�� ![]() ��t=2ʱ����P������ABCD�ı�BC��1�������㣻
��t=2ʱ����P������ABCD�ı�BC��1�������㣻
��4 ![]() ��6��t��1ʱ����P���BC��2�������㣮
��6��t��1ʱ����P���BC��2�������㣮
����������1������BD��AC��O������ֱ��������AOB���������εĶԽ����ഹֱ���Խ���ƽ�ֶԽǡ��ڱ���ȵ�������֪��PAQ�ס�CAB��Ȼ����ݡ����������εĶ�Ӧ����ȡ�֤�á�APQ=��ACB��������ƽ���ߵ��ж�������ͬλ����ȣ���ֱ��ƽ�С�����֤�ý��ۣ���2����ͼ2����P��BC���ڵ�M������PM������Rt��CPM����Rt��CPM��������ǵ����Ǻ���ֵ���PM= ![]() PC=
PC= ![]() ��Ȼ�����PM=PQ=AQ=t�г�����t�ķ��̣�ͨ���ⷽ�̼������t��ֵ�� ��ͼ3����P����B����ʱPQ=PB�����ݵȱ������ε��ж�������֪��PQBΪ�ȱ������Σ�Ȼ���ɵȱ������ε������Լ���2�������t��ֵ��ȷ����ʱt��ȡֵ��Χ��
��Ȼ�����PM=PQ=AQ=t�г�����t�ķ��̣�ͨ���ⷽ�̼������t��ֵ�� ��ͼ3����P����B����ʱPQ=PB�����ݵȱ������ε��ж�������֪��PQBΪ�ȱ������Σ�Ȼ���ɵȱ������ε������Լ���2�������t��ֵ��ȷ����ʱt��ȡֵ��Χ��
��ͼ4����P����C����ʱPC=PQ���ݴ˵�����ϵ�г�����t�ķ��̣�ͨ���ⷽ�����t��ֵ��


 Сѧ�������Ծ�ϵ�д�
Сѧ�������Ծ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ijѧУ��չ��Զ�Ǿ�ɽ��ĥ����־���������࣬������Ϊ�����Զ������֪ѧУ���ɽ�����24ǧ�ף�Զ�������Ա�����г���ѧ�����У�������Ա�����г���ƽ���ٶ���ѧ������ƽ���ٶȵ�2.5����������Ա��ѧ��ͬʱ��ѧУ�����������ɽ��ʱ��������Ա����ʱ���ѧ��������3.6Сʱ����ѧ�����е�ƽ���ٶ��Ƕ���ǧ��/Сʱ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��һ����ֵת������

(1)������x��25ʱ���������y��ֵ��
(2)�Ƿ��������x��ֵ��ʼ���䲻��y��ֵ��������ڣ���ֱ��д����������Ҫ���xֵ����������ڣ���˵�����ɣ�
(3)����һ����λ��x��ǡ�þ�������ȡ����ƽ�����������������y����x��________(ֻ��һ������)��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڱ߳�Ϊ24cm��������ֽƬABCD�ϣ���ȥͼ����Ӱ���ֵ��ĸ�ȫ�ȵĵ���ֱ�������Σ�����ͼ�е����������۳�һ����������״�İ�װ�У�A��B��C��D�ĸ����������غ����ϵ�����һ�㣩����֪E��F��AB���ϣ��DZ���ȥ��һ������ֱ��������б�ߵ������˵㣬��AE=BF=x��cm���� 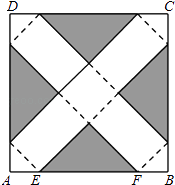
��1�����۳ɵİ�װ��ǡ���Ǹ������壬���������װ�е����V��
��2��ij�����Ҫ���װ�еı��棨�����µ��棩���S�������xӦȡ��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��һ����¥�ײ�B��ɽ��Pλ��ͬһˮƽ���ϣ�С����P����þ���¥��A������Ϊ60�㣬Ȼ������P�����½�Ϊ45���ɽ�������ߵ�C������ʱ��PC=30m����C���A��ͬһˮƽ���ϣ�A��B��P��C��ͬһƽ���ڣ�
��1�������¥AB�ĸ߶ȣ�
��2����C��A֮��ľ��룮
����ȷ��0.1m���ο����ݣ� ![]() ��1.41��
��1.41�� ![]() ��1.73��
��1.73�� ![]() ��2.45��
��2.45��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������зḻ�����β�Ʒ��ijУ���꼶��1�����ͬѧ�Ͳ������β�Ʒ��ϲ��������ο�������飬Ҫ���ο����оٵ����β�Ʒ��ѡ��ϲ���IJ�Ʒ����ֻ��ѡһ�������ͬѧ�������IJ�������ͳ��ͼ�� 
����������Ϣ����������⣺
��1���뽫����ͳ��ͼ����������
��2�����������ο����ˣ�������ͳ��ͼ�У�A������ռ��Բ�Ľ����ȣ�
��3������ݵ�����������1500���ο���ϲ���ʽ���Լ���ˣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������
��1����ͼ��1����P��������ABCD�ı�CD��һ�㣨��P���C��D���غϣ�����E��BC���ӳ����ϣ���CE=CP������BP��DE����֤����BCP�ա�DCE�� 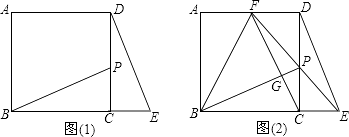
��2��ֱ��EP��AD��F������BF��FC����G��FC��BP�Ľ��㣮 ����CD=2PCʱ����֤��BP��CF��
����CD=nPC��n�Ǵ���1��ʵ����ʱ���ǡ�BPF�����ΪS1 �� ��DPE�����ΪS2 �� ��֤��S1=��n+1��S2 ��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com