
【题目】(题型一)请你参与下面的探究过程,完成所提出的问题.
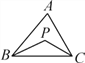
(1)探究1:如图11-3-3(1),P是△ ABC的内角∠ABC与∠ACB的平分线BP和CP的交点,若∠A=70°,求∠BPC度数.
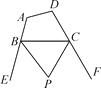
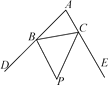
(2)探究2:如图11-3-3(2),P是△ABC的外角∠DBC与外角∠ECB的平分线BP和CP的交点,求∠BPC与∠A的数量关系,并说明理由.边形ABCD的外角∠EBC与∠BCF的平分线BP和CP的交点,设∠A+∠D=α.
①直接写出∠BPC与α的数量关系;
②根据α值的情况,判断△BPC的形状.(按角分类)
(1) (2) (3)
【答案】(1)∠BPC=125°;
(2)∠BPC=90°-![]() ∠A.理由见解析;
∠A.理由见解析;
(3)当0°<α<180°时,△BPC是钝角三角形;当α=180°时,△BPC是直角三角形;当α>180°时,△BPC是锐角三角形.
【解析】试题分析:(1)先根据三角形内角和定理求出∠ABC+∠ACB的度数,再根据角平分线的性质求出∠PBC+∠BCP的度数,由三角形内角和定理即可求出答案;
(2)根据角平分线的定义可得∠PCE=![]() ∠BCE,∠PBD=
∠BCE,∠PBD=![]() ∠CBD,然后根据三角形内角和定理列式整理即可得解;
∠CBD,然后根据三角形内角和定理列式整理即可得解;
(3)①根据四边形的内角和定理表示出∠BAD+∠CDA,然后同理(2)解答即可;②根据α的值的情况,得到∠P的取值范围,即可得到结论.
试题解析:(1)∵∠A=70°,
∴∠ABC+∠ACB=180°-∠A=110°.
∵BP,CP分别是∠ABC,∠ACB的平分线,
∴∠ABC=2∠PBC,∠ACB=2∠BCP,
∴∠PBC+∠BCP=1/2(∠ABC+∠ACB)=55°.
∵∠PBC+∠BCP+∠BPC=180°,
∴∠BPC=125°.
(2)∠BPC=90°-![]() ∠A.
∠A.
理由:∵BP,CP分别是外角∠DBC,∠ECB的平分线,
∴∠PBC+∠PCB=![]() (∠DBC+∠ECB)=
(∠DBC+∠ECB)=![]() (180°+∠A).
(180°+∠A).
在△PBC中,∠BPC=180°-![]() (180°+∠A)=90°-
(180°+∠A)=90°-![]() ∠A.
∠A.
(3)如图,
①延长BA,CD交于点Q,
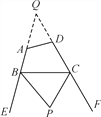
由(2)可知,∠BPC=90°-![]() ∠Q,
∠Q,
∴∠Q=180°-2∠BPC,
∴∠BAD+∠CDA=180°+∠Q=180°+180°-2∠BPC=360°-2∠BPC.
∴∠BPC=180°-![]() α.
α.
②当0°<α<180°时,△BPC是钝角三角形;
当α=180°时,△BPC是直角三角形;
当α>180°时,△BPC是锐角三角形.


科目:初中数学 来源: 题型:
【题目】为了节约水资源,某市准备按照居民家庭年用水量实行阶梯水价.水价分档递增,计划使第一档、第二档和第三档的水价分别覆盖全市居民家庭的80%,15%和5%,为合理确定各档之间的界限,随机抽查了该市5万户居民家庭上一年的年用水量(单位:m3),绘制了统计图.如图所示,下面四个推断( )
①年用水量不超过180m3的该市居民家庭按第一档水价交费;
②年用水量超过240m3的该市居民家庭按第三档水价交费;
③该市居民家庭年用水量的中位数在150﹣180之间;
④该市居民家庭年用水量的平均数不超过180.
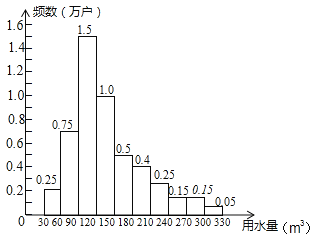
A.①③ B.①④ C.②③ D.②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校初三(1)班部分同学接受一次内容为“最适合自己的考前减压方式”的调查活动,收集整理数据后,老师将减压方式分为五类,并绘制了图1、图2两个不完整的统计图,请根据图中的信息解答下列问题.
(1)初三(1)班接受调查的同学共有多少名;
(2)补全条形统计图,并计算扇形统计图中的“体育活动C”所对应的圆心角度数;
(3)若喜欢“交流谈心”的5名同学中有三名男生和两名女生;老师想从5名同学中任选两名同学进行交流,直接写出选取的两名同学都是女生的概率.
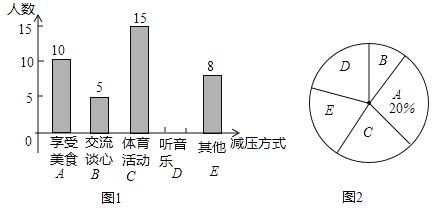
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,△ABC的三个顶点的坐标分别为A(-3,4),B(-4,2),C(-2,1),且△A1B1C1与△ABC关于原点O成中心对称。
(1)画出△A1B1C1,并写出点A1的坐标;
(2)P(a,b)是△ABC的AC边上一点,△ABC经平移后点P的对应点为P'(a+3,b+1),请画出平移后的△A2B2C2.
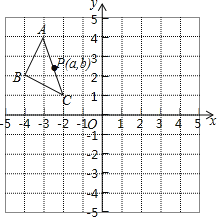
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com