
【题目】如图1,![]() 与
与![]() 都是等腰直角三角形,直角边
都是等腰直角三角形,直角边![]() ,
,![]() 在同一条直线上,点
在同一条直线上,点![]() 、
、![]() 分别是斜边
分别是斜边![]() 、
、![]() 的中点,点
的中点,点![]() 为
为![]() 的中点,连接
的中点,连接![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
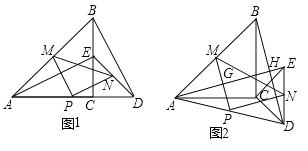
(1)观察猜想:
图1中,![]() 与
与![]() 的数量关系是______,位置关系是______.
的数量关系是______,位置关系是______.
(2)探究证明:
将图1中的![]() 绕着点
绕着点![]() 顺时针旋转
顺时针旋转![]() ,得到图2,
,得到图2,![]() 与
与![]() 、
、![]() 分别交于点
分别交于点![]() 、
、![]() ,判断
,判断![]() 的形状,并说明理由;
的形状,并说明理由;
(3)拓展延伸:
把![]() 绕点
绕点![]() 任意旋转,若
任意旋转,若![]() ,
,![]() ,请直接写出
,请直接写出![]() 面积的最大值.
面积的最大值.
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]() 的形状为等腰直角三角形,理由见解析;(3)
的形状为等腰直角三角形,理由见解析;(3)![]() 的面积的最大值为
的面积的最大值为![]() .
.
【解析】
(1)延长AE交BD于点H,易证ΔACE≌ΔBCD,得AE=BD,∠CAE=∠CBD,进而得∠BHA=90°,结合中位线的性质,得PM=![]() BD,PM//BD,PN=
BD,PM//BD,PN=![]() AE, PN//AE,进而得PM=PN,PM⊥PN;
AE, PN//AE,进而得PM=PN,PM⊥PN;
(2)设AE交BC于⊙O,易证ΔACE≌ΔBCD,得AE=BD,∠CAE=∠CBD,进而得∠BHA=90°,结合中位线的性质,得PM=![]() BD,PM//BD,PN=
BD,PM//BD,PN=![]() AE, PN//AE,进而得PM=PN,PM⊥PN;
AE, PN//AE,进而得PM=PN,PM⊥PN;
(3)易证ΔPMN是等腰直角三角形,PM=![]() BD,当B、C、D共线时,BD的值最大,进而求解.
BD,当B、C、D共线时,BD的值最大,进而求解.
解:(1)如图1,
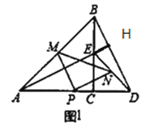
延长AE交BD于点H,
∵ΔACB和ΔECD是等腰直角三角形,
∴AC=BC,EC=CD,
∠ACB=∠ECD=90°,
∴∠ACB+∠BCE=∠ECD+∠BCE,
∴∠ACE=∠BCD,
∴ΔACE≌ΔBCD(SAS),
∴AE=BD,∠CAE=∠CBD,
又∵∠AEC=∠BEH,
∴∠BHA=∠ACE=90°,
∵点P、M、N分别为AD、AB、DE的中点,
∴PM=![]() BD,PM//BD,PN=
BD,PM//BD,PN=![]() AE,PN//AE,
AE,PN//AE,
∴PM=PN,
∴PM⊥AH,
∴PM⊥PN.
(2)如图中,设![]() 交
交![]() 于
于![]() .
.
∵![]() 和
和![]() 是等腰直角三角形,
是等腰直角三角形,
∴![]() ,
,![]() ,
,![]()
∴![]()
∴![]() .∴
.∴![]()
∴![]() ,
,![]()
又∵![]() ,
,![]() ,∴
,∴![]()
∵点![]() 、
、![]() 、
、![]() 分别为
分别为![]() 、
、![]() 、
、![]() 的中点,∴
的中点,∴![]() ,
,![]() ;
;
![]() ,
,![]() .∴
.∴![]()
∴![]()
∴![]()
∴![]()
∴![]()
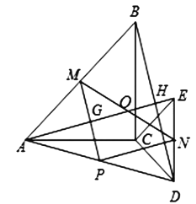
(3)![]() 的面积的最大值为
的面积的最大值为![]() .
.
由(2)可知![]() 是等腰直角三角形,
是等腰直角三角形,![]() ,
,
∴当![]() 的值最大时,
的值最大时,![]() 的值最大,
的值最大,![]() 的面积最大,
的面积最大,
∴当![]() 、
、![]() 、
、![]() 共线时,
共线时,![]() 的最大值
的最大值![]() ,∴
,∴![]() ,
,
∴![]() 的面积的最大值
的面积的最大值![]() .
.


科目:初中数学 来源: 题型:
【题目】题目:某校七年级学生乘车去参加社会实践活动,若每辆客车乘50人,还有12人不能上车;若每辆客车乘55人,则最后一辆空了8个座位,求该校租这种客车的辆数:
根据题意,小明、小红分别列出了尚不完整的方程如下:
小明列出不完整的方程为![]()
小红列出不完整的方程为![]()
(说明:其中“![]() ”表示运算符号,“
”表示运算符号,“![]() ”表示数字):
”表示数字):
(1)小明所列方程中![]() 表示的意义是________________________;
表示的意义是________________________;
小红所列方程中![]() 表示的意义是___________________________;
表示的意义是___________________________;
(2)选择两位同学的其中一位学生的做法,将其补充完整,并完整地解答这道题.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】王老师为了解同学们对金庸武侠小说的阅读情况,随机对初三年级的部分同学进行调查,将调查结果分成以下五类:A:看过0~3本,B:看过4~6本,C:看过7~9本,D:看过10~12本,E:看过13~15本.并根据调查结果绘制了如图1、图2两幅不完整的统计图.
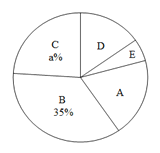
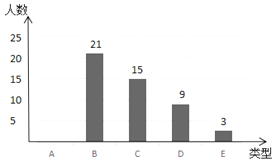
(1)图2中的a = ,D所对的圆心角度数为 °;
(2)请补全条形统计图;
(3)本次调查中E类有2男1女,王老师想从中抽取2名同学分别撰写一篇读书笔记.请用列表或画树状图的方法求所抽取的两名学生恰好是一男一女的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,BC>AB>AC,D是边BC上的一个动点(点D不与点B、C重合),将△ABC沿AD折叠,点B落在点B'处,连接BB',B'C,若△BCB'是等腰三角形,则符合条件的点D的个数是
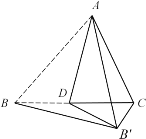
A. 0个B. 1个C. 2个D. 3个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:当点P在射线OA上时,把![]() 的的值叫做点P在射线OA上的射影值;当点P不在射线OA上时,把射线OA上与点P最近点的射影值,叫做点P在射线OA上的射影值.
的的值叫做点P在射线OA上的射影值;当点P不在射线OA上时,把射线OA上与点P最近点的射影值,叫做点P在射线OA上的射影值.
例如:如图1,△OAB三个顶点均在格点上,BP是OA边上的高,则点P和点B在射线OA上的射影值均为![]() =
=![]() .
.

(1)在△OAB中,
①点B在射线OA上的射影值小于1时,则△OAB是锐角三角形;
②点B在射线OA上的射影值等于1时,则△OAB是直角三角形;
③点B在射线OA上的射影值大于1时,则△OAB是钝角三角形.
其中真命题有 .
A.①②B.①③C.②③D.①②③
(2)已知:点C是射线OA上一点,CA=OA=1,以〇为圆心,OA为半径画圆,点B是⊙O上任意点.
①如图2,若点B在射线OA上的射影值为![]() .求证:直线BC是⊙O的切线;
.求证:直线BC是⊙O的切线;
②如图3,已知D为线段BC的中点,设点D在射线OA上的射影值为x,点D在射线OB上的射影值为y,直接写出y与x之间的函数关系式为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,直线l:y=x+1与y轴交于点A1,如图所示,依次作正方形OA1B1C1,正方形C1A2B2C2,正方形C2A3B3C3,正方形C3A4B4C4,……,点A1,A2,A3,A4,……在直线l上,点C1,C2,C3,C4,……在x轴正半轴上,则前n个正方形对角线长的和是____________.
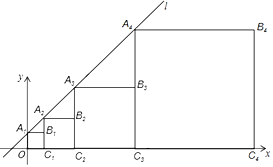
查看答案和解析>>
科目:初中数学 来源: 题型:
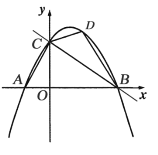
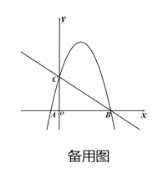
【题目】如图,在平面直角坐标系中,直线![]() 分别与
分别与![]() 轴、
轴、![]() 轴相交于点B、C,经过点B、C的抛物线
轴相交于点B、C,经过点B、C的抛物线![]() 与
与![]() 轴的另一个交点为A.
轴的另一个交点为A.
(1)求出抛物线表达式,并求出点A坐标;
(2)已知点D在抛物线上,且横坐标为3,求出△BCD的面积;
(3)点P是直线BC上方的抛物线上一动点,过点P作PQ垂直于![]() 轴,垂足为Q.是否存在点P,使得以点A、P、Q为顶点的三角形与△BOC相似?若存在,请求出点P的坐标;若不存在,请说明理由.
轴,垂足为Q.是否存在点P,使得以点A、P、Q为顶点的三角形与△BOC相似?若存在,请求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
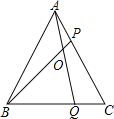
【题目】如图,在等边三角形ABC的AC,BC边上各取一点P,Q,使AP=CQ,AQ,BP相交于点O.若BO=6,PO=2,则AP的长,AO的长分别为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,△ABC的三个顶点坐标分别为A(2,1),B(1,4),C(3,2).请解答下列问题:
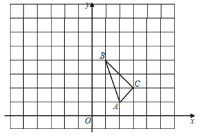
(1)画出△ABC关于y轴对称的图形△A1B1C1,并直接写出C1点的坐标;
(2)以原点O为位似中心,位似比为1:2,在y轴的右侧,画出△ABC放大后的图形△A2B2C2,并直接写出C2点的坐标;
(3)如果点D(a,b)在线段BC上,请直接写出经过(2)的变化后对应点D2的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com