
【题目】定义:在平面直角坐标系中,![]() 为坐标原点,
为坐标原点,![]() 的边
的边![]() 平行于
平行于![]() 轴.若
轴.若![]() 的三个顶点都在二次函数
的三个顶点都在二次函数![]() 的图像上,则称
的图像上,则称![]() 为该二次函数图像的“伴随三角形”.
为该二次函数图像的“伴随三角形”.![]() 为抛物
为抛物![]() 的“伴随三角形”.
的“伴随三角形”.
(1)若点![]() 是抛物线与
是抛物线与![]() 轴的交点,求点
轴的交点,求点![]() 的坐标.
的坐标.
(2)若点![]() 在该抛物线的对称轴上,且到边
在该抛物线的对称轴上,且到边![]() 的距离为2,求
的距离为2,求![]() 的面积.
的面积.
(3)设![]() 两点的坐标分别为
两点的坐标分别为![]() ,比较
,比较![]() 与
与![]() 的大小,并求
的大小,并求![]() 的取值范围.
的取值范围.
(4)![]() 是抛物线
是抛物线![]() 的“伴随三角形”,点
的“伴随三角形”,点![]() 在点
在点![]() 的左侧,且
的左侧,且![]() ,点
,点![]() 的横坐标是点
的横坐标是点![]() 的横坐标的2倍,设该抛物线在
的横坐标的2倍,设该抛物线在![]() 上最高点的纵坐标为
上最高点的纵坐标为![]() ,当
,当![]() 时,直接写出
时,直接写出![]() 的取值范围和
的取值范围和![]() 面积的最大值.
面积的最大值.
【答案】(1)![]() ;(2)4;(3)当
;(2)4;(3)当![]() 时,
时,![]() ,当
,当![]() ,
,![]() 且
且![]() 时,
时,![]() ;(4)
;(4)![]() ,
,![]()
【解析】
(1)由![]() 轴及伴随三角形的定义,抛物线的对称轴可得答案.
轴及伴随三角形的定义,抛物线的对称轴可得答案.
(2)由题意得:![]() 为抛物线的顶点,求解
为抛物线的顶点,求解![]() 的坐标,结合已知条件,得到
的坐标,结合已知条件,得到![]() 的坐标,进而求出
的坐标,进而求出![]() 与
与![]() 上的高可得
上的高可得![]() 的面积.
的面积.
(3)先写出![]() 两点坐标,由
两点坐标,由![]() 轴,当
轴,当![]() 为抛物线的顶点时,
为抛物线的顶点时,![]() 不存在,当
不存在,当![]() 两点的纵坐标相等时,
两点的纵坐标相等时,![]() 不存在,求解对应的
不存在,求解对应的![]() 的值,再利用二次函数的性质分段得到答案,
的值,再利用二次函数的性质分段得到答案,
(4)由![]() 求解抛物线的对称轴
求解抛物线的对称轴![]() ,分
,分![]() 讨论最高点的位置,求解最高点在纵坐标,代入
讨论最高点的位置,求解最高点在纵坐标,代入![]() ,利用二次函数的性质求解
,利用二次函数的性质求解![]() 的范围,再求解
的范围,再求解![]() 面积的最大值.
面积的最大值.
(1)当![]() 时,
时,![]() ,∴
,∴![]()
对称轴: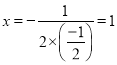 ,
,
![]() 轴,
轴,
∴![]()
(2)![]() 在抛物线上,也在对称轴上,
在抛物线上,也在对称轴上,
![]() 为抛物线的顶点,
为抛物线的顶点,
当![]() 时,
时,![]()
∴![]()
![]() 到边
到边![]() 的距离为2,
的距离为2,
∴![]()
∴当![]() 时,
时,![]()
![]() ,
,![]()
∴![]() ,
,![]()
∴![]()
∴![]()
(3)![]() ,
,![]()
①当![]() 时,
时,![]() 为抛物线的顶点,所以
为抛物线的顶点,所以![]() 不成立,
不成立,
②当![]()
解得:![]() ,
,![]() ,
,
此时结合题意:![]() 轴,
轴,![]() 不成立
不成立
③当![]() 时,如图
时,如图
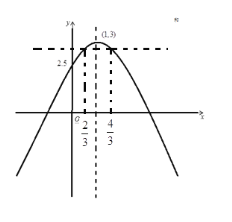
结合图像得:![]() ,
,
④当![]() 且
且![]() 时,结合图像可得:
时,结合图像可得:![]()
⑤当![]() 时,结合图像可得:
时,结合图像可得:![]()
综上:
当![]() 时,
时,![]()
当![]() ,
,![]() 且
且![]() 时,
时,![]() .
.
(4)![]()
![]()
![]()
![]()
顶点![]()
①当![]() 时,即
时,即![]()
当![]() 时
时
![]()
![]()
![]()
![]()
当![]()
![]()
解得:![]()
由二次函数的性质得:![]()
由![]() ,
,
![]()
![]()
![]()
![]()
![]() 为任意数
为任意数
∴![]()
②当![]() 时,
时,
即:![]() ,顶点的纵坐标最大,
,顶点的纵坐标最大,
![]()
![]() ,
,
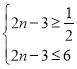
∴![]()
综上![]()
当![]() 时,
时,![]()
![]() 轴,
轴,
![]()
![]() 此时
此时![]() ,
,
![]()
当![]() 时,
时,![]() ,
,
当![]() 时,
时,![]() 时
时
![]()
![]()
∴![]()
此时面积最大,最大面积是![]()


科目:初中数学 来源: 题型:
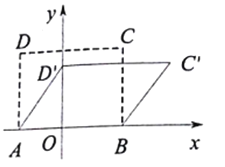
【题目】四边形具有不稳定性,如图,在平面直角坐标系![]() 中,矩形
中,矩形![]() 的边
的边![]() 在
在![]() 轴上,且点
轴上,且点![]() ,边
,边![]() 长为
长为![]() .现固定边
.现固定边![]() ,向右推动矩形使点
,向右推动矩形使点![]() 落在
落在![]() 轴上(落点记为
轴上(落点记为![]() ),点
),点![]() 的对应点记为
的对应点记为![]() ,已知矩形
,已知矩形![]() 与推动后形成的平行四边形
与推动后形成的平行四边形![]() 的面积比为
的面积比为![]() ,则点
,则点![]() 坐标为_______.
坐标为_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
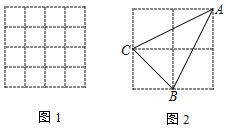
【题目】如图1,每个小正方形的边长都为1,点A、B、C在正方形网格的格点上,AB=5,AC=2,BC=![]() .
.
(1)请在网格中画出△ABC
(2)如图2,直接写出:
①AC= ,BC= .
②△ABC的面积为 .
③AB边上的高为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下表是小安填写的数学实践活动报告的部分内容
题 目 | 测量铁塔顶端到地面的高度 | |
测量目标示意图 |
|
|
相关数据 | CD=20m,ɑ=45°,β=52° | |
求铁塔的高度FE(结果精确到1米)(参考数据:sin52°≈0.79, cos52°≈0.62,tan52°≈1.28)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】题目:为了美化环境,某地政府计划对辖区内![]() 的土地进行绿化.为了尽快完成任务,实际平均每月的绿化面积是原计划的1.5倍,结果提前2个月完成任务.求原计划平均每月的绿化面积.
的土地进行绿化.为了尽快完成任务,实际平均每月的绿化面积是原计划的1.5倍,结果提前2个月完成任务.求原计划平均每月的绿化面积.
甲同学所列的方程为![]()
乙同学所列的方程为![]()
(1)甲同学所列的方程中![]() 表示 .乙同学所列的方程中
表示 .乙同学所列的方程中![]() 表示 .
表示 .
(2)任选甲、乙两同学的其中一个方法解答这个题目.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲乙两个工厂同时加工一批机器零件.甲工厂先加工了两天后停止加工,维修设备,当维修完设备时,甲乙两厂加工的零件数相等,甲工厂再以原来的工作效率继续加工这批零件.甲乙两厂加工零件的数量![]() (件),
(件),![]() (件)与加工件的时间
(件)与加工件的时间![]() (天)的函数图象如图所示,
(天)的函数图象如图所示,

(1)乙工厂每天加工零件的数为_____件;
(2)甲工厂维修设备的时间是多少天?
(3)求甲维修设备后加工零件的数量![]() (件)与加工零件的时间
(件)与加工零件的时间![]() (天)的函数关系式,并写出自变量
(天)的函数关系式,并写出自变量![]() 的取值范围
的取值范围
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,抛物线![]() 与
与![]() 轴交于
轴交于![]() 、
、![]() 两点,与直线
两点,与直线![]() 交于
交于![]() 、
、![]() 两点,直线
两点,直线![]() 与
与![]() 轴交于点
轴交于点![]() .
.
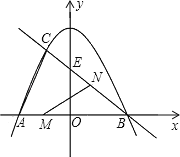
(1)求直线![]() 的解析式:
的解析式:
(2)若点![]() 在线段
在线段![]() 上以每秒1个单位长度的速度从点
上以每秒1个单位长度的速度从点![]() 向点
向点![]() 运动(不与点
运动(不与点![]() 、
、![]() 重合),同时,点
重合),同时,点![]() 在射线
在射线![]() 上以每秒2个单位长度的速度从点
上以每秒2个单位长度的速度从点![]() 向点
向点![]() 方向运动,设运动的时间为
方向运动,设运动的时间为![]() 秒,
秒,![]() 的面积为
的面积为![]() ,求
,求![]() 关于
关于![]() 的函数关系式,并求
的函数关系式,并求![]() 取何值时,
取何值时,![]() 最大?最大值是多少?
最大?最大值是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图点A,E,F,C在同一直线上,AE=EF=FC,过E,F分别作DE⊥AC,BF⊥AC,连结AB,CD,BD,BD交AC于点G,若AB=CD.
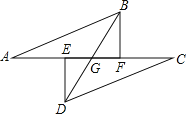
(1)求证:△ABF≌△CDE.
(2)若AE=ED=2,求BD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某种蔬菜的销售单价y1与销售月份x之间的关系如图(1)所示,成本y2与销售月份之间的关系如图(2)所示(图(1)的图象是线段图(2)的图象是抛物线)
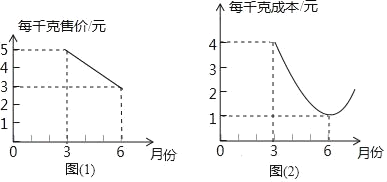
(1)分别求出y1、y2的函数关系式(不写自变量取值范围);
(2)通过计算说明:哪个月出售这种蔬菜,每千克的收益最大?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com