
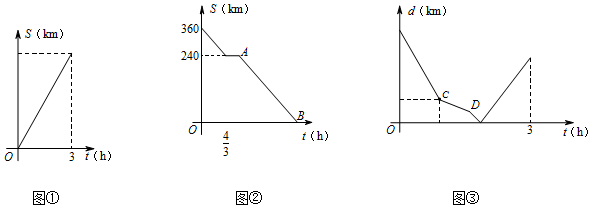
分析 (1)观察图象可知AB=360km,根据速度=$\frac{路程}{时间}$计算即可;
(2)求出A、B两点坐标,利用待定系数法即可解决问题;
(3)①求出t=$\frac{4}{3}$h时,两车之间的距离即可解决问题;
②客车停在C站的时候,轿车与客车的距离随时间的变化情况.
解答 解:(1)观察图象可知:AB=360km,
$\frac{360}{3}$=120km/h,
故答案为360,120.
(2)由题可知,A($\frac{5}{3}$,240),
客车速度为(360+240)÷$\frac{4}{3}$=90km/h
停留后继续行驶了$\frac{240}{90}$=$\frac{8}{3}$
B($\frac{13}{3}$,0)
设AB的函数关系式S=kt+b(k≠0)
$\left\{\begin{array}{l}240=\frac{5}{3}k+b\\ 0=\frac{13}{3}k+b\end{array}$
解得,$\left\{\begin{array}{l}k=-90\\ b=390\end{array}$
即S=-90t+390($\frac{5}{3}$≤t≤$\frac{13}{3}$),
(3)①t=$\frac{4}{3}$时,两车之间的距离=360-120-120×$\frac{4}{3}$=80,
∴C( $\frac{4}{3}$,80).
②客车停在C站的时候,轿车与客车的距离随时间的变化情况.
故答案为($\frac{4}{3}$,80).
点评 本题考查一次函数的应用、待定系数法、路程、速度、时间之间的关系等知识,解题的关键是读懂图象信息,灵活运用所学知识解决问题.


科目:初中数学 来源: 题型:选择题
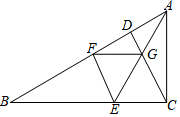 如图,在直角△ABC中,∠ACB=Rt∠,∠B=30°,CD为斜边AB上的高线,折叠△ABC使得AC落在AB上,点C与点F重合,展开的折痕AE交CD于点G,连接FG、EF.下列结论:①图中有6对全等三角形;②BC=6DG;③若将△EFG沿FG所在的直线折叠,则点E必在直线CD上;④AG=EF;⑤图中共有5个等腰直角三角形,其中正确的结论的个数是( )
如图,在直角△ABC中,∠ACB=Rt∠,∠B=30°,CD为斜边AB上的高线,折叠△ABC使得AC落在AB上,点C与点F重合,展开的折痕AE交CD于点G,连接FG、EF.下列结论:①图中有6对全等三角形;②BC=6DG;③若将△EFG沿FG所在的直线折叠,则点E必在直线CD上;④AG=EF;⑤图中共有5个等腰直角三角形,其中正确的结论的个数是( )| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (-3)-(+1)=-4 | B. | (-3)+(+1)=-2 | C. | (+3)+(-1)=+2 | D. | (+3)+(+1)=+4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com