
【题目】如图,直线![]() 交
交![]() 轴于A点,交
轴于A点,交![]() 轴于B点,过A、B两点的抛物线交x轴于另一点C(3,0).
轴于B点,过A、B两点的抛物线交x轴于另一点C(3,0).
⑴求抛物线的解析式;
⑵在抛物线的对称轴上是否存在点Q,使△ABQ是等腰三角形?若存在,求出符合条件的Q点坐标;若不存在,请说明理由.
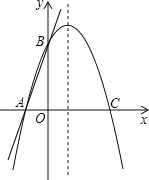
【答案】(1)此抛物线的解析式为y=-(x+1)(x-3)=-x2+2x+3;
(2)Q点坐标为(1,1),(1,0),(1,![]() ),(1,﹣
),(1,﹣![]() ).
).
【解析】
(1)根据直线的解析式y=3x+3,当x=0和y=0时就可以求出点A、B的坐标,设抛物线的解析式为y=ax2+bx+c,根据A、B、C三点的坐标利用待定系数法就可以求出抛物线的解析式;
(2)将抛物线化为顶点式,求出对称轴对称轴,设出Q点的坐标,利用等腰三角形的性质,根据两点间的距离公式就可以求出Q点的坐标.
(1)∵y=3x+3,
∴当x=0时,y=3,当y=0时,x=﹣1,
∴A(﹣1,0),B(0,3).
设抛物线的解析式为y=ax2+bx+c,由题意,得
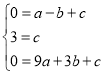 ,
,
解得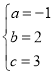
∴抛物线的解析式为:y=﹣x2+2x+3
(2)∵y=﹣x2+2x+3,
∴y=﹣(x﹣1)2+4
∴抛物线的对称轴为x=1,设Q(1,a),
①当AQ=BQ时,如图,
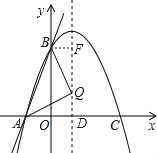
由勾股定理可得
BQ=![]() ,
,
AQ=![]()
得![]() ,
,
解得a=1,
∴Q(1,1);
②如图:
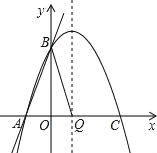
当AB是腰时,Q是对称轴与x轴交点时,AB=BQ,
∴![]()
![]()
解得:a=0或6,
当Q点的坐标为(1,6)时,其在直线AB上,A、B和Q三点共线,舍去,
则此时Q的坐标是(1,0);
③当AQ=AB时,如图:
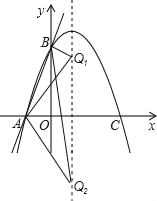
![]() ,解得a=±
,解得a=±![]() ,则Q的坐标是(1,
,则Q的坐标是(1,![]() )和(1,﹣
)和(1,﹣![]() ).
).
综上所述:Q点坐标为(1,1),(1,0),(1,![]() ),(1,﹣
),(1,﹣![]() ).
).


科目:初中数学 来源: 题型:
【题目】黄石市在创建国家级文明卫生城市中,绿化档次不断提升.某校计划购进A,B两种树木共100棵进行校园绿化升级,经市场调查:购买A种树木2棵,B种树木5棵,共需600元;购买A种树木3棵,B种树木1棵,共需380元.
(1)求A种,B种树木每棵各多少元?
(2)因布局需要,购买A种树木的数量不少于B种树木数量的3倍.学校与中标公司签订的合同中规定:在市场价格不变的情况下(不考虑其他因素),实际付款总金额按市场价九折优惠,请设计一种购买树木的方案,使实际所花费用最省,并求出最省的费用.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】①当a=2,b=﹣3时,分别求代数式a2﹣2ab+b2和(a﹣b)2的值.
②当a=﹣![]() ,b=﹣2.25时,分别求代数式a2﹣2ab+b2和(a﹣b)2的值.
,b=﹣2.25时,分别求代数式a2﹣2ab+b2和(a﹣b)2的值.
③猜想这两个代数式的值有何关系?
④根据猜想用简便方法算出当a=2018,b=2021时,代数式a2﹣2ab+b2的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是某小组做用频率估计概率“的实验时,绘出的某一结果出现的频率折线图,则符合这一结果的实验可能是( )
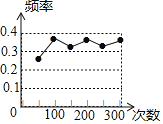
A. 抛一枚硬币,出现正面朝上
B. 从一个装有2个红球1个黑球的袋子中任取一球,取到的是黑球
C. 一副去掉大小王的扑克牌洗匀后,从中任抽一张牌的花色是红桃
D. 掷一枚均匀的正六面体骰子,出现3点朝上
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】己知二次函数y=ax2+bx+c的y与x的部分对应值如下表;
x | -1 | 0 | 1 | 3 |
y | -3 | 1 | 3 | 1 |
下列结论:①抛物线的开口向下;②其图象的对称轴为x=1;③当x﹤l时,函数值y随x 的增大而增大;④方程ax2+bx+c=0有一个根大于4.其中正确的结论有( )
A. 4个B. 1个C. 3个D. 2个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,AB=10cm,BC=8cm,点P从点A沿AC向点C以1cm/s的速度运动,同时点Q从点C沿CB向点B以2cm/s的速度运动(点Q运动到点B停止),在运动过程中,四边形PABQ的面积最小值为()cm2.
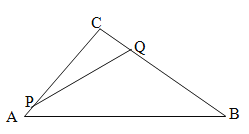
A. 19 B. 16 C. 15 D. 12
查看答案和解析>>
科目:初中数学 来源: 题型:
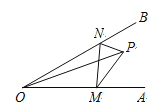
【题目】如图,∠AOB![]() 30°,点P是∠AOB内的一定点,且OP
30°,点P是∠AOB内的一定点,且OP![]() 6,若点M,N分别是射线OA,OB上异于点O的动点,则△PMN周长的最小值是__________.
6,若点M,N分别是射线OA,OB上异于点O的动点,则△PMN周长的最小值是__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】仙桃是遂宁市某地的特色时令水果.仙桃一上市,水果店的老板用2400元购进一批仙桃,很快售完;老板又用3700元购进第二批仙桃,所购件数是第一批的![]() 倍,但进价比第一批每件多了5元.
倍,但进价比第一批每件多了5元.
(1)第一批仙桃每件进价是多少元?
(2)老板以每件225元的价格销售第二批仙桃,售出80%后,为了尽快售完,剩下的决定打折促销.要使得第二批仙桃的销售利润不少于440元,剩余的仙桃每件售价至少打几折?(利润=售价﹣进价)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com