
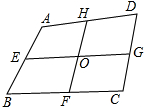
 在四边形ABCD中,点E,F,G,H,分别是AB,BC,CD,DE的中点,EG与FH相交于O点.
在四边形ABCD中,点E,F,G,H,分别是AB,BC,CD,DE的中点,EG与FH相交于O点.| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |


科目:初中数学 来源: 题型:
 为了加强公民的节约意识,我市出台阶梯电价计算方案:(如下图)居民生活用电将月用电量分为三档,第一档为月用电量200度(含)以内,第二档为月用电量200~320度(含),第三档为月用电量320度以上.这三个档次的电价分别为:第一档0.52元/度,第二档0.57元/度,第三档0.82元/度.若某户居民1月份用电250度,则应收电费:0.52×200+0.57×(250-200)=132.5元.
为了加强公民的节约意识,我市出台阶梯电价计算方案:(如下图)居民生活用电将月用电量分为三档,第一档为月用电量200度(含)以内,第二档为月用电量200~320度(含),第三档为月用电量320度以上.这三个档次的电价分别为:第一档0.52元/度,第二档0.57元/度,第三档0.82元/度.若某户居民1月份用电250度,则应收电费:0.52×200+0.57×(250-200)=132.5元.查看答案和解析>>
科目:初中数学 来源: 题型:
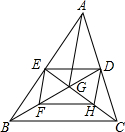 △ABC的两条中线BD与CE交于点G、F、H分别是BG、CG的中点,连接DE、EF、F、HD.
△ABC的两条中线BD与CE交于点G、F、H分别是BG、CG的中点,连接DE、EF、F、HD.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com