练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
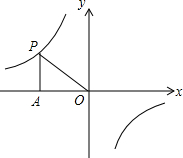
    3．如图，已知点P是双曲线y=$\frac{k}{x}$（k≠0）上一点，过点P作PA⊥x轴于点A，且S△PAO=2，则该双曲线的解析式为（　　）
    A．y=-$\frac{4}{x}$B．y=-$\frac{2}{x}$C．y=$\frac{4}{x}$D．y=$\frac{2}{x}$

    分析 先判断出k的符号，再由反比例函数系数k的几何意义即可得出结论．

    解答 解：∵反比例函数的图象在二四象限，
    ∴k＜0．
    ∵PA⊥x轴于点A，且S△PAO=2，
    ∴k=-4，
    ∴反比例函数的解析式为y=-$\frac{4}{x}$．
    故选A．

    点评 本题考查的是用待定系数法求反比例函数的解析式，熟知反比例函数系数k的几何意义是解答此题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

    13．对于数据：6，3，4，7，6，0，9，下列判断中正确的是（　　）
    A．这组数据的平均数是6，中位数是6B．这组数据的平均数是5，中位数是6
    C．这组数据的平均数是6，中位数是7D．这组数据的平均数是5，中位数是7

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    14．分解因式：3a2-6a+3=3（a-1）2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

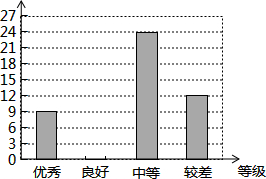    11．为进一步加强学习贯彻2015年新修订的《中小学生守则》，某校组织全校学生参加安溪县中小学“学守则•促文明•行规范”校园猜谜比赛，将比赛成绩分为“优秀、良好、中等、较差”四个等级．现从中随机抽取该校部分学生的比赛成绩进行统计分析，并制成了如下的统计图表：
    比赛成绩等级人数百分比
    较差12b
    中等24c
    良好a25%
    优秀915%
    根据图表信息，回答下列问题：
    （1）本次抽查的学生共有60名；
    （2）统计表中所表示的数a=15，b=20%，并将条形统计图补充完整；
    （3）已知该校共有1800名学生参加比赛，请你估计比赛成绩达到“良好”或“优秀”等级的人数约是多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    18．如图，AD∥BE∥CF，直线l1，l2与三条平行线分别交于点A，B，C和点D，E，F．若AC=3，BC=2，DE=1.5，则DF的长为4.5．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    8．下列各式正确的是（　　）
    A．x2+x3=x5B．x3•x2=2x5C．x5÷x3=x2D．（x5）2=x7

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

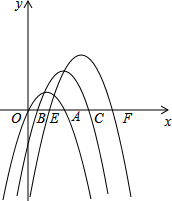    15．已知，如图，将抛物线y1=-（x-1）2+1，y2=-（x-2）2+2，y3=-（x-3）2+3，…，yn=-（x-n）2+n（n为正整数）称为“系列抛物线”，其分别与x轴交于点O，A，B，C，E，F，…．
    （1）①抛物线y1的顶点坐标为（1，1）；
    ②该“系列抛物线”的顶点在直线y=x上；
    ③yn=-（x-n）2+n与x轴的两交点之间的距离是2$\sqrt{n}$．
    （2）是否存在整数n，使以yn=-（x-n）2+n的顶点及该抛物线与x轴两交点为顶点的三角形是等边三角形？
    （3）以yn=-（x-n）2+n的顶点P为一个顶点作该二次函数图象的内接等边△PMN（M，N两点在该二次函数的图象上），请问：△PMN的面积是否会随着n的变化而变化？若不会，请求出这个等边三角形的面积；若会，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    12．在一个凸n边形的纸板上切下一个三角形后，剩下的一个内角和为1080°的多边形，则n的值为（　　）
    A．7B．8C．9D．以上都有可能

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    13．解不等式组$\left\{\begin{array}{l}x-3（x-2）≤4\\ \frac{1+2x}{3}＞x-1\end{array}\right.$，并把它的解集在数轴上表示出来．

    查看答案和解析>>

    同步练习册答案