
【题目】如图,点A、B在反比例函数![]() 的图象上,且点A、B的横坐标分别为a、2a(a>0),AC⊥x轴,垂足为C,且△AOC的面积为2,
的图象上,且点A、B的横坐标分别为a、2a(a>0),AC⊥x轴,垂足为C,且△AOC的面积为2,
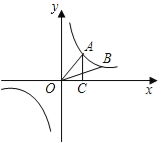
(1)求该反比例函数的解析式;
(2)求△AOB的面积.
科目:初中数学 来源: 题型:
【题目】已知,矩形ABCD中,AB=4cm,BC=8cm,AC的垂直平分线EF分别交AD、BC于点E、F,垂足为O.
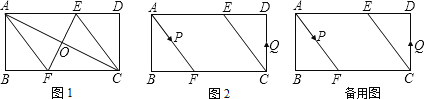
(1)如图1,连接AF、CE.求证四边形AFCE为菱形,并求AF的长;
(2)如图2,动点P、Q分别从A、C两点同时出发,沿△AFB和△CDE各边匀速运动一周.即点P自A→F→B→A停止,点Q自C→D→E→C停止.在运动过程中,
①已知点P的速度为每秒5cm,点Q的速度为每秒4cm,运动时间为t秒,当A、C、P、Q四点为顶点的四边形是平行四边形时,求t的值.
②若点P、Q的运动路程分别为a、b(单位:cm,ab≠0),已知A、C、P、Q四点为顶点的四边形是平行四边形,求a与b满足的数量关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b与反比例函数y=![]() 的图象相交于A(2,3),B(﹣3,n)两点.
的图象相交于A(2,3),B(﹣3,n)两点.

(1)求一次函数与反比例函数的解析式;
(2)根据所给条件,请直接写出不等式kx+b>![]() 的解集;
的解集;
(3)过点B作BC⊥x轴,垂足为C,求S△ABC.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,长方形ABCD中,AB=10cm,BC=8cm,点E是CD的中点,动点P从A点出发,以每秒2cm的速度沿A→B→C→E运动,最终到达点E.若点P运动的时间为x秒,那么当x= 时,△APE的面积等于32.
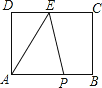
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若一个直角三角形的一条直角边长是7 cm,另一条直角边比斜边短1 cm,则斜边长 ( )
A. 18 cm B. 20 cm C. 24 cm D. 25 cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的袋子里装有若干个红球和黄球,这些球除颜色外完全相同.从中任意摸出一个球,记下颜色后放回,搅匀后再重新摸球,则下列说法中正确的是( )
A.摸到黄球的频数越大,摸到黄球的频率越大
B.摸到黄球的频数越大,摸到黄球的频率越小
C.重复多次摸球后,摸到黄球的频数逐渐稳定
D.重复多次摸球后,摸到黄球的频率逐渐稳定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】木匠师傅锯木料时,一般先在木板上画出两个点,然后过这两点弹出一条墨线,这是因为( )
A.两点之间,线段最短
B.两点确定一条直线
C.两点之间线段的长度,叫做这两点之间的距离
D.圆上任意两点间的部分叫做圆弧
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,设图中每个小正方形的边长为1,
(1)请画出△ABC关于y轴对称图形△A’B’C’,其中ABC的对称点分别为A’B’C’)
(2)直接写出A’B’C’的坐标:A’B’C’
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com