
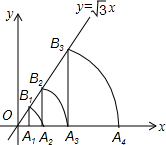
 如图,直线y=$\sqrt{3}$x,点A1坐标为(1,0),过点A1作x轴的垂线交直线于点B1,以原点O为圆心,OB1长为半径画弧交x轴于点A2;再过点A2作x轴的垂线交直线于点B2,以原点O为圆心,OB2长为半径画弧交x轴于点A3,…,按照此做法进行下去,点A6的坐标为(32,0).
如图,直线y=$\sqrt{3}$x,点A1坐标为(1,0),过点A1作x轴的垂线交直线于点B1,以原点O为圆心,OB1长为半径画弧交x轴于点A2;再过点A2作x轴的垂线交直线于点B2,以原点O为圆心,OB2长为半径画弧交x轴于点A3,…,按照此做法进行下去,点A6的坐标为(32,0). 分析 在Rt△OA1B1中,由OA1=1、A1B1=$\sqrt{3}$OA1=$\sqrt{3}$,利用勾股定理可得出OB1=2,进而可得出点A2的坐标为(2,0),同理,即可求出点A3、A4、A5、A6的坐标,此题得解.
解答 解:在Rt△OA1B1中,OA1=1,A1B1=$\sqrt{3}$OA1=$\sqrt{3}$,
∴OB1=$\sqrt{O{{A}_{1}}^{2}+{A}_{1}{{B}_{1}}^{2}}$=2,
∴点A2的坐标为(2,0).
同理,可得出:点A3的坐标为(4,0),点A4的坐标为(8,0),点A5的坐标为(16,0),点A6的坐标为(32,0).
故答案为:(32,0).
点评 本题考查了一次函数图象上点的坐标特征、解直角三角形以及规律型中点的坐标,根据一次函数图象上点的坐标特征结合解直角三角形,求出点A2、A3、A4、A5、A6的坐标是解题的关键.


 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
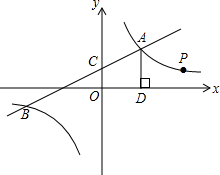 如图,一次函数y1=k1x+b与反比例函数y2=$\frac{{k}_{2}}{x}$的图象交于点A(4,m)和B(-8,-2),与y轴交于点C.
如图,一次函数y1=k1x+b与反比例函数y2=$\frac{{k}_{2}}{x}$的图象交于点A(4,m)和B(-8,-2),与y轴交于点C.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
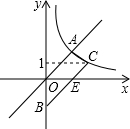 如图,梯形AOBC的顶点A,C在反比例函数图象上,OA∥BC,上底边OA在直线y=x上,下底边BC交y轴于B(0,-4),则四边形AOBC的面积为2$\sqrt{5}$+10.
如图,梯形AOBC的顶点A,C在反比例函数图象上,OA∥BC,上底边OA在直线y=x上,下底边BC交y轴于B(0,-4),则四边形AOBC的面积为2$\sqrt{5}$+10.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
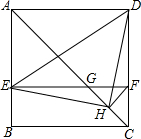 如图,在正方形ABCD中,AC为对角线,E为AB上一点,过点E作EF∥AD,与AC、DC分别交于点G、F,H为CG的中点,连接DE、EH、DH、FH.下列结论:①EG=DF;②∠AEH+∠ADH=180°;③△EHF≌△DHC;④若$\frac{AE}{AB}$=$\frac{1}{3}$,则3S△EDH=13S△DHC,其中结论正确的有①②③(填写序号).
如图,在正方形ABCD中,AC为对角线,E为AB上一点,过点E作EF∥AD,与AC、DC分别交于点G、F,H为CG的中点,连接DE、EH、DH、FH.下列结论:①EG=DF;②∠AEH+∠ADH=180°;③△EHF≌△DHC;④若$\frac{AE}{AB}$=$\frac{1}{3}$,则3S△EDH=13S△DHC,其中结论正确的有①②③(填写序号).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com