
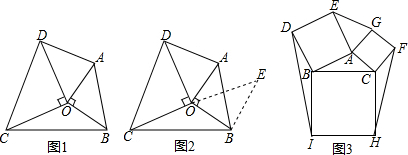
分析 由等腰直角三角形的性质、旋转的性质知,△OEB与△BOC是等底同高的两个三角形,由此即可解决问题.
(1)将△DBI和△FCH平移即可得到如图所示的△EGM.
(2)如图2,根据正方形的性质推知△ABE和△ACG都是等腰直角三角形,则根据旋转的性质推知S△AEG=S△AEM=S△AMG=S△ABC=1,所以易求△EGM的面积.
解答 解:∵△ABO和△CDO均为等腰直角三角形,∠AOB=∠COD=90°,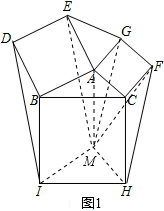
∴OD=OC,OA=OB.
又∵∠BOE+∠AOE=90°,∠AOD+∠AOE=90°,
∴∠AOD=∠BOE,
∴△OBE≌△OAD,
∴△BCE即是以AD、BC、OC+OD的长度为三边长的三角形.
∵△OEB与△BOC是等底同高的两个三角形,
∴S△OEB=S△BOC=1,
∴S△BCE=S△OEB+S△BOC=2.
故答案为2.
(1)(答案不唯一):如图1,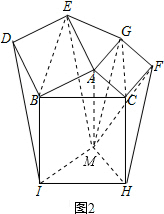
以EG、FH、ID的长度为三边长的一个三角形是△EGM.
(2)如图2,∵四边形AEDB和四边形ACFG都是正方形,
∴△ABE和△ACG都是等腰直角三角形,
∴S△AEG=S△AEM=S△AMG=S△ABC=1,
∴S△EGM=S△AEG+S△AEM+S△AMG=3,即以EG、FH、ID的长度为三边长的三角形的面积等于3.
故答案为3.
点评 本题考查了全等三角形的判定与性质、三角形的面积、等腰三角形的性质以及正方形的性质等知识,解题的关键是平移、旋转的性质的应用,想办法移动这些分散的线段,构造一个三角形,属于中考压轴题.


科目:初中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -3 | B. | -2 | C. | 0 | D. | 1 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 55°,55° | B. | 55°,70° | ||
| C. | 70°,40° | D. | 55°,55°或70°,40° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 了解某班同学的身高情况适合用全面调查 | |
| B. | 数据4、5、5、6、0的平均数是5 | |
| C. | 数据2、3、4、2、3的中位数是4 | |
| D. | 甲、乙两组数据的平均数相同,方差分别是S甲2=3.2,S乙2=2.9,则甲组数据更稳定 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -$\frac{5}{2}$ | B. | -$\frac{2}{5}$ | C. | $\frac{5}{2}$ | D. | $\frac{2}{5}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
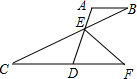 如图AB∥CD,AD与BC交于点E,EF平分∠BED交CD延长线于点F,若∠A=110°,∠B=30°,则∠F的度数是( )
如图AB∥CD,AD与BC交于点E,EF平分∠BED交CD延长线于点F,若∠A=110°,∠B=30°,则∠F的度数是( )| A. | 20° | B. | 30° | C. | 40° | D. | 50° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com