
【题目】如图,![]() 是边长为6的等边三角形,
是边长为6的等边三角形,![]() 是
是![]() 边上一动点,由
边上一动点,由![]() 向
向![]() 运动(与
运动(与![]() 、
、![]() 不重合),
不重合),![]() 是
是![]() 延长线上一动点,与点
延长线上一动点,与点![]() 同时以相同的速度由
同时以相同的速度由![]() 向
向![]() 延长线方向运动(
延长线方向运动(![]() 不与
不与![]() 重合),过
重合),过![]() 作
作![]() 于
于![]() ,连接
,连接![]() 交
交![]() 于
于![]() .
.

(1)当![]() 时,求
时,求![]() 的长;
的长;
(2)在运动过程中线段![]() 的长是否发生变化?如果不变,求出线段
的长是否发生变化?如果不变,求出线段![]() 的长;如果发生改变,请说明理由.
的长;如果发生改变,请说明理由.
【答案】(1)2;(2)不变,DE=3为定值.
【解析】
(1)过P作PF∥QC,证明△DBQ≌△DFP,根据全等三角形的性质计算即可;
(2)根据等边三角形的性质、直角三角形的性质解答.
(1)解:过P作PF∥QC,
则△AFP是等边三角形,
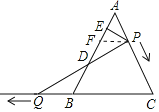
∵P、Q同时出发,速度相同,即BQ=AP,
∴BQ=PF,
在△DBQ和△DFP中,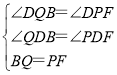 ,
,
∴△DBQ≌△DFP,
∴BD=DF,
∵∠BQD=∠BDQ=∠FDP=∠FPD=30°,
∴BD=DF=FA=![]() AB=2,
AB=2,
∴AP=2;
(2)解:由(1)知BD=DF,
∵△AFP是等边三角形,PE⊥AB,
∴AE=EF,
∴DE=DF+EF=![]() BF+
BF+![]() FA=
FA=![]() AB=3为定值,即DE的长不变.
AB=3为定值,即DE的长不变.


科目:初中数学 来源: 题型:
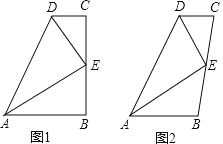
【题目】如图,E 是 BC 的中点,DE 平分∠ADC.
(1)如图 1,若∠B=∠C=90°,求证:AE 平分∠DAB;
(2)如图 2,若 DE⊥AE,求证:AD=AB+CD.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将两块斜边长相等的等腰直角三角板按如图①摆放,斜边AB分别交CD,CE于M,N点.
(1)如果把图①中的△BCN绕点C逆时针旋转90°得到△ACF,连接FM,如图②,求证:△CMF≌△CMN;
(2)将△CED绕点C旋转,则:
①当点M,N在AB上(不与点A,B重合)时,线段AM,MN,NB之间有一个不变的关系式,请你写出这个关系式,并说明理由;
②当点M在AB上,点N在AB的延长线上(如图③)时,①中的关系式是否仍然成立?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一个安装有进出水管的30升容器,水管单位时间内进出的水量是一定的,设从
某时刻开始的4分钟内只进水不出水,在随后的8分钟内既进水又出水,得到水量y(升)
与时间x(分)之间的函数关系如图所示.根据图象信息给出下列说法:
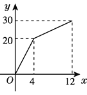
①每分钟进水5升;②当4≤x≤12时,容器中水量在减少;
③若12分钟后只放水,不进水,还要8分钟可以把水放完;
④若从一开始进出水管同时打开需要24分钟可以将容器灌满.
以上说法中正确的有( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
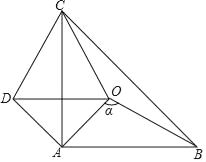
【题目】如图,△ABC和△AOD是等腰直角三角形,AB=AC,AO=AD,∠BAC=∠OAD=90°,点O是△ABC内的一点,∠BOC=130°.
(1)求证:OB=DC;
(2)求∠DCO的大小;
(3)设∠AOB=α,那么当α为多少度时,△COD是等腰三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一次800米的长跑比赛中,甲、乙两人所跑的路程![]() (米)与各自所用时间
(米)与各自所用时间![]() (秒)之间的函数图像分别为线段
(秒)之间的函数图像分别为线段![]() 和折线
和折线![]() ,则下列说法不正确的是( )
,则下列说法不正确的是( )

A.甲的速度保持不变B.乙的平均速度比甲的平均速度大
C.在起跑后第180秒时,两人不相遇D.在起跑后第50秒时,乙在甲的前面
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,以
,以![]() 为直径的
为直径的![]() 交
交![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() ,在
,在![]() 上取一点
上取一点![]() ,使
,使![]() ,连接
,连接![]() ,对于下列结论:①
,对于下列结论:①![]() ;②
;②![]() ;③弧
;③弧![]() 弧
弧![]() ;④
;④![]() 为
为![]() 的切线,结论一定正确的是( )
的切线,结论一定正确的是( )

A. ②③ B. ②④ C. ①② D. ①③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“端午”节前,第一次爸爸去超市购买了大小、质量都相同的火腿粽子和豆沙粽子若干,放入不透明的盒中,此时随机取出火腿粽子的概率为![]() ;妈妈发现小亮喜欢吃的火腿粽子偏少,第二次妈妈又去买了同样的
;妈妈发现小亮喜欢吃的火腿粽子偏少,第二次妈妈又去买了同样的![]() 只火腿粽子和
只火腿粽子和![]() 只豆沙粽子放入同一盒中,这时随机取出火腿粽子的概率为
只豆沙粽子放入同一盒中,这时随机取出火腿粽子的概率为![]() .
.
![]() 请计算出第一次爸爸买的火腿粽子和豆沙粽子各有多少只?
请计算出第一次爸爸买的火腿粽子和豆沙粽子各有多少只?
![]() 若妈妈从盒中取出火腿粽子
若妈妈从盒中取出火腿粽子![]() 只、豆沙粽子
只、豆沙粽子![]() 只送爷爷和奶奶后,再让小亮从盒中不放回地任取
只送爷爷和奶奶后,再让小亮从盒中不放回地任取![]() 只,问恰有火腿粽子、豆沙粽子各
只,问恰有火腿粽子、豆沙粽子各![]() 只的概率是多少?(用字母和数字表示豆沙粽子和火腿粽子,用列清法计算)
只的概率是多少?(用字母和数字表示豆沙粽子和火腿粽子,用列清法计算)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com