
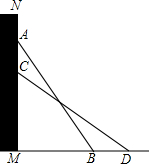
 如图,把一个长为10m的梯子AB斜靠在墙上,测得AM=8m,BM=6m,梯子沿墙下滑到CD位置,测得∠ABM=∠DCM,求梯子下滑的高度.
如图,把一个长为10m的梯子AB斜靠在墙上,测得AM=8m,BM=6m,梯子沿墙下滑到CD位置,测得∠ABM=∠DCM,求梯子下滑的高度. 科目:初中数学 来源: 题型:解答题
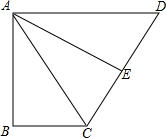 已知,如图,Rt△ABC中,∠B=90°,AB=6,BC=4,以斜边AC为底边作等腰三角形ACD,腰AD刚好满足AD∥BC,并作腰上的高AE.
已知,如图,Rt△ABC中,∠B=90°,AB=6,BC=4,以斜边AC为底边作等腰三角形ACD,腰AD刚好满足AD∥BC,并作腰上的高AE.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在如图所示网格内建立恰当直角坐标系后,画出函数y=2x2和y=-$\frac{1}{2}$x2的图象,并根据图象回答下列问题(设小方格的边长为1).
在如图所示网格内建立恰当直角坐标系后,画出函数y=2x2和y=-$\frac{1}{2}$x2的图象,并根据图象回答下列问题(设小方格的边长为1).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com