
·ÖÎö £¨1£©Ôʽ·ÖĸÓÐÀí»¯¼ÆËã¼´¿ÉµÃµ½½á¹û£»
£¨2£©ÔʽÀûÓöþ´Î¸ùʽ³ý·¨·¨Ôò¼ÆËã¼´¿ÉµÃµ½½á¹û£»
£¨3£©Ôʽ·ÖĸÓÐÀí»¯¼ÆËã¼´¿ÉµÃµ½½á¹û£»
£¨4£©Ôʽ·ÖĸÓÐÀí»¯¼ÆËã¼´¿ÉµÃµ½½á¹û£»
£¨5£©Ôʽ·ÖĸÓÐÀí»¯¼ÆËã¼´¿ÉµÃµ½½á¹û£»
£¨6£©ÔʽÀûÓöþ´Î¸ùʽ³ý·¨·¨Ôò¼ÆËã¼´¿ÉµÃµ½½á¹û£»
£¨7£©ÔʽÀûÓöþ´Î¸ùʽ³Ë³ý·¨Ôò¼ÆËã¼´¿ÉµÃµ½½á¹û£®
½â´ð ½â£º£¨1£©Ôʽ=$\sqrt{\frac{48}{6}}$=$\sqrt{8}$=2$\sqrt{2}$£»
£¨2£©Ôʽ=$\sqrt{\frac{3}{5}¡Á30}$=$\sqrt{18}$=3$\sqrt{2}$£»
£¨3£©Ôʽ=$\frac{\sqrt{3}¡Á\sqrt{7}}{\sqrt{7}¡Á\sqrt{7}}$=$\frac{\sqrt{21}}{7}$£»
£¨4£©Ôʽ=$\frac{2\sqrt{3}¡Á\sqrt{2}}{\sqrt{8}¡Á\sqrt{2}}$=$\frac{\sqrt{6}}{2}$£»
£¨5£©Ôʽ=$\frac{\sqrt{15}¡Á\sqrt{3x}}{\sqrt{3x}¡Á\sqrt{3x}}$=$\frac{3\sqrt{5x}}{3x}$=$\frac{\sqrt{5x}}{x}$£»
£¨6£©Ôʽ=$\sqrt{\frac{b}{5}•\frac{20{a}^{2}}{b}}$=|2a|£»
£¨7£©Ôʽ=$\sqrt{27¡Á50¡Â6}$=$\sqrt{225}$=15£®
µãÆÀ ´ËÌ⿼²éÁË·ÖĸÓÐÀí»¯£¬ÒÔ¼°¶þ´Î¸ùʽµÄ³Ë³ý·¨£¬ÊìÁ·ÕÆÎÕ¶þ´Î¸ùʽ³Ë³ý·¨ÔòÊǽⱾÌâµÄ¹Ø¼ü£®


 ÌìÌìÏòÉÏÒ»±¾ºÃ¾íϵÁдð°¸
ÌìÌìÏòÉÏÒ»±¾ºÃ¾íϵÁдð°¸ СѧÉú10·ÖÖÓÓ¦ÓÃÌâϵÁдð°¸
СѧÉú10·ÖÖÓÓ¦ÓÃÌâϵÁдð°¸ Ä¿±ê²âÊÔϵÁдð°¸
Ä¿±ê²âÊÔϵÁдð°¸
| Ä꼶 | ¸ßÖÐ¿Î³Ì | Ä꼶 | ³õÖÐ¿Î³Ì |
| ¸ßÒ» | ¸ßÒ»Ãâ·Ñ¿Î³ÌÍƼö£¡ | ³õÒ» | ³õÒ»Ãâ·Ñ¿Î³ÌÍƼö£¡ |
| ¸ß¶þ | ¸ß¶þÃâ·Ñ¿Î³ÌÍƼö£¡ | ³õ¶þ | ³õ¶þÃâ·Ñ¿Î³ÌÍƼö£¡ |
| ¸ßÈý | ¸ßÈýÃâ·Ñ¿Î³ÌÍƼö£¡ | ³õÈý | ³õÈýÃâ·Ñ¿Î³ÌÍƼö£¡ |
¿ÆÄ¿£º³õÖÐÊýѧ À´Ô´£º ÌâÐÍ£º½â´ðÌâ
²é¿´´ð°¸ºÍ½âÎö>>
¿ÆÄ¿£º³õÖÐÊýѧ À´Ô´£º ÌâÐÍ£ºÌî¿ÕÌâ
 Èçͼ£¬Ð¡·½¸ñÊDZ߳¤Îª1µÄÕý·½ÐΣ¬ÔòËıßÐÎABCDµÄÖܳ¤Îª15+3$\sqrt{5}$+$\sqrt{26}$£®
Èçͼ£¬Ð¡·½¸ñÊDZ߳¤Îª1µÄÕý·½ÐΣ¬ÔòËıßÐÎABCDµÄÖܳ¤Îª15+3$\sqrt{5}$+$\sqrt{26}$£®²é¿´´ð°¸ºÍ½âÎö>>
¿ÆÄ¿£º³õÖÐÊýѧ À´Ô´£º ÌâÐÍ£ºÌî¿ÕÌâ
²é¿´´ð°¸ºÍ½âÎö>>
¿ÆÄ¿£º³õÖÐÊýѧ À´Ô´£º ÌâÐÍ£º½â´ðÌâ
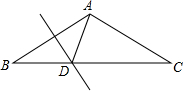 Èçͼ£¬AB=AC£¬¡ÏBAC=120¡ã£¬ABµÄ´¹Ö±Æ½·ÖÏß½»BCÓÚµãD£®
Èçͼ£¬AB=AC£¬¡ÏBAC=120¡ã£¬ABµÄ´¹Ö±Æ½·ÖÏß½»BCÓÚµãD£®²é¿´´ð°¸ºÍ½âÎö>>
¿ÆÄ¿£º³õÖÐÊýѧ À´Ô´£º ÌâÐÍ£º½â´ðÌâ
²é¿´´ð°¸ºÍ½âÎö>>
¿ÆÄ¿£º³õÖÐÊýѧ À´Ô´£º ÌâÐÍ£º½â´ðÌâ
²é¿´´ð°¸ºÍ½âÎö>>
¿ÆÄ¿£º³õÖÐÊýѧ À´Ô´£º ÌâÐÍ£º½â´ðÌâ
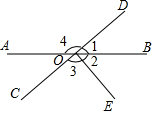 Èçͼ£¬Ö±ÏßAB£¬CDÏཻÓÚµãO£¬ÇÒ¡Ï1=¡Ï2£¬ÒÑÖª¡Ï2£º¡Ï3=2£º5£¬Çó¡Ï4¡¢¡ÏAOCµÄ¶ÈÊý£®
Èçͼ£¬Ö±ÏßAB£¬CDÏཻÓÚµãO£¬ÇÒ¡Ï1=¡Ï2£¬ÒÑÖª¡Ï2£º¡Ï3=2£º5£¬Çó¡Ï4¡¢¡ÏAOCµÄ¶ÈÊý£®²é¿´´ð°¸ºÍ½âÎö>>
¿ÆÄ¿£º³õÖÐÊýѧ À´Ô´£º2017½ì½ËÕÊ¡ÎÞÎýÊоÅÄ꼶ÏÂѧÆÚµÚÒ»´ÎÄ£Ä⿼ÊÔÊýѧÊÔ¾í£¨½âÎö°æ£© ÌâÐÍ£ºÌî¿ÕÌâ
Èçͼ£¬¡÷ABCÈý¸ö¶¥µãµÄ×ø±ê·Ö±ðΪA£¨2£¬2£©£¬B£¨4£¬2£©£¬C£¨6£¬4£©£¬ÒÔÔµãOΪλËÆÖÐÐÄ£¬½«¡÷ABCËõСΪÔÀ´µÄÒ»°ë£¬ÔòÏ߶ÎACµÄÖеãP±ä»»ºóÔÚµÚÒ»ÏóÏÞ¶ÔÓ¦µãµÄ×ø±êΪ______£®

²é¿´´ð°¸ºÍ½âÎö>>
°Ù¶ÈÖÂÐÅ - Á·Ï°²áÁбí - ÊÔÌâÁбí
ºþ±±Ê¡»¥ÁªÍøÎ¥·¨ºÍ²»Á¼ÐÅÏ¢¾Ù±¨Æ½Ì¨ | ÍøÉÏÓк¦ÐÅÏ¢¾Ù±¨×¨Çø | µçÐÅթƾٱ¨×¨Çø | ÉæÀúÊ·ÐéÎÞÖ÷ÒåÓк¦ÐÅÏ¢¾Ù±¨×¨Çø | ÉæÆóÇÖȨ¾Ù±¨×¨Çø
Î¥·¨ºÍ²»Á¼ÐÅÏ¢¾Ù±¨µç»°£º027-86699610 ¾Ù±¨ÓÊÏ䣺58377363@163.com