
【题目】如图1,小红将一张直角梯形纸片沿虚线剪开,得到矩形和三角形两张纸片,测得AB=15,AD=12.在进行如下操作时遇到了下面的几个问题,请你帮助解决.
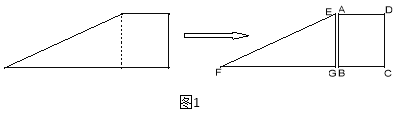
(1)将△EFG的顶点G移到矩形的顶点B处,再将三角形绕点B顺时针旋转使E点落在CD边上,此时,EF恰好经过点A(如图2)求FB的长度
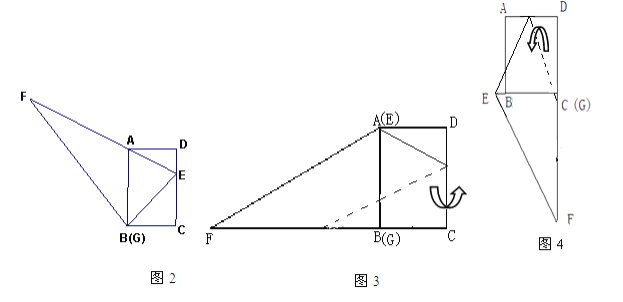
(2)在(1)的条件下,小红想用△EFG包裹矩形ABCD,她想了两种包裹的方法如图3、图4,请问哪种包裹纸片的方法使得未包裹住的面积大?(纸片厚度忽略不计)请你通过计算说服小红。
【答案】(1)30;(2) 二种包裹纸片的方法使得未包裹住的面积相等.
【解析】
试题分析:(1)利用矩形的性质以及得出△ADE∽△FBE,求出即可;
(2)根据Rt△F,HN~Rt△F,EG,得到HN=3,从而S△AMH=144;由Rt△GBE~Rt△C,B,G,得到GB,=24,从而S△B,C,G=144,进行比较即可.
⑴BE=AD=15,在RtBCE中,CE2=B E2-BC2=152-122,求得CE=9,DE=6,
证Rt△ADE~Rt△FBE,
求得BF=30
⑵①如图1,将矩形ABCD和Rt△FBE以CD为轴翻折,则△AMH即为未包裹住的面积,

由Rt△F,HN~Rt△F,EG,得到HN=3,
从而S△AMH=144
②如图2,将矩形ABCD和Rt△ECF以AD为轴翻折,由Rt△GBE~Rt△C,B,G,得到GB,=24,

从而S△B,C,G=144,∴未包裹的面积为144.
∴按照二种包裹的方法未包裹的面积相等。


 同步练习强化拓展系列答案
同步练习强化拓展系列答案科目:初中数学 来源: 题型:
【题目】一根祝寿蜡烛长85 cm,点燃时每小时缩短5 cm.
(1)请写出点燃蜡烛的长y(cm)与蜡烛燃烧时间t(h)之间的函数关系式;
(2)该蜡烛可点燃多长时间?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】实践与探索:将连续的奇数1,3,5,7…排列成如图的数表用十字框框出5个数(如图) 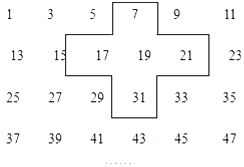
(1)若将十字框上下左右平移,但一定要框住数列中的5个数,若设中间的数为a,用a的代数式表示十字框框住的5个数字之和;
(2)十字框框住的5个数之和能等于2015吗?若能,分别写出十字框框住的5个数;若不能,请说明理由;
(3)十字框框住的5个数之和能等于365吗?若能,分别写出十字框框住的5个数;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ACE是以□ABCD的对角线AC为边的等边三角形,点C与点E关于x轴对称.若E点的坐标是(7,-3 ![]() ),则D点的坐标是 ( )
),则D点的坐标是 ( )
A.(4,0)
B.( ![]() ,0)
,0)
C.(5,0)
D.( ![]() ,0)
,0)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,①②③④⑤五个平行四边形拼成一个含30度内角的菱形EFGH(不重叠无缝隙).若①②③④四个平行四边形面积的和为26cm2 , 四边形ABCD面积是19cm2 , 则①②③④四个平行四边形周长的总和为( )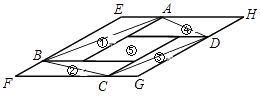
A.96cm
B.64cm
C.48cm
D.36cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A的坐标为(-1,0),点B的坐标为(4,0),经过点A点B抛物线y=x+bx+c与y轴交于点C.
(1)求抛物线的关系式.
(2)△ABC的外接圆与y轴交于点D,在抛物线上是否存在点M使S△MBC=S△DBC,若存在,请求出点M的坐标.
(3)点P是直线y=-x上一个动点,连接PB,PC,当PB+PC+PO最小时,求点P的坐标及其最小值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A是y轴正半轴上的一个定点,点B是反比例函数y=![]() (k为常数)在第一象限内图象上的一个动点.当点B的纵坐标逐渐增大时,△OAB的面积( )
(k为常数)在第一象限内图象上的一个动点.当点B的纵坐标逐渐增大时,△OAB的面积( )
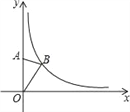
A. 逐渐减小 B. 逐渐增大 C. 先增大后减小 D. 不变
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com