
分析 如果一个数是智慧数,就能表示为两个正整数的平方差,设这两个数分别m、n,设m>n,即智慧数=m2-n2=(m+n)(m-n),因为m,n是正整数,因而m+n和m-n就是两个自然数.要判断一个数是否是智慧数,可以把这个数分解因数,分解成两个整数的积,看这两个数能否写成两个正整数的和与差.
解答 解:1不能表示为两个正整数的平方差,所以1不是“智慧数”.对于大于1的奇正整数2k+1,有2k+1=(k+1)2-k2(k=1,2,…).所以大于1的奇正整数都是“智慧数”.
对于被4整除的偶数4k,有4k=(k+1)2-(k-1)2(k=2,3,…).
即大于4的被4整除的数都是“智慧数”,而4不能表示为两个正整数平方差,所以4不是“智慧数”.
对于被4除余2的数4k+2(k=0,1,2,3,…),设4k+2=x2-y2=(x+y)(x-y),其中x,y为正整数,
当x,y奇偶性相同时,(x+y)(x-y)被4整除,而4k+2不被4整除;
当x,y奇偶性相异时,(x+y)(x-y)为奇数,而4k+2为偶数,总得矛盾.
所以不存在自然数x,y使得x2-y2=4k+2.即形如4k+2的数均不为“智慧数”.
因此,在正整数列中前四个正整数只有3为“智慧数”,此后,每连续四个数中有三个“智慧数”.
因为2017=(1+3×672),4×(672+1)=2692,所以2692是第2017个“智慧数”,
故答案为:2692.
点评 本题主要考查了平方差公式,有一定的难度,主要是对题中新定义的理解与把握.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:填空题
 如图,将边长为4的正方形ABCD沿其对角线AC剪开,固定△ADC,并把△ABC沿着AD方向平移,得到△A′B′C′,当两个三角形重叠部分的面积为2时,它移动的距离AA′等于2+$\sqrt{2}$或2-$\sqrt{2}$.
如图,将边长为4的正方形ABCD沿其对角线AC剪开,固定△ADC,并把△ABC沿着AD方向平移,得到△A′B′C′,当两个三角形重叠部分的面积为2时,它移动的距离AA′等于2+$\sqrt{2}$或2-$\sqrt{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
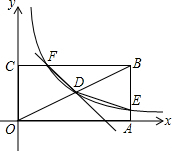 如图,矩形OABC的顶点A,C分别在x,y轴的正半轴上,D为对角线OB的中点,反比例函数y=$\frac{k}{x}$在第一象限内的图象经过点D,且与AB、BC分别交于点E,F,点B的坐标为(2$\sqrt{3}$,2).
如图,矩形OABC的顶点A,C分别在x,y轴的正半轴上,D为对角线OB的中点,反比例函数y=$\frac{k}{x}$在第一象限内的图象经过点D,且与AB、BC分别交于点E,F,点B的坐标为(2$\sqrt{3}$,2).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在平面直角坐标系中,点A的坐标为(3,0),B为直线y=$\frac{\sqrt{3}}{3}$x上的一个动点,延长AB至C,使得AB=BC,过点C作CD⊥x轴于点D,交直线OB于点F,过点A作AE∥OB,交直线CD于点E.
如图,在平面直角坐标系中,点A的坐标为(3,0),B为直线y=$\frac{\sqrt{3}}{3}$x上的一个动点,延长AB至C,使得AB=BC,过点C作CD⊥x轴于点D,交直线OB于点F,过点A作AE∥OB,交直线CD于点E.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com