
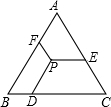
 如图所示,△ABC是等边三角形,P是其内任意一点,PD∥AB,PE∥BC,PF∥AC,若△ABC的周长为24,则PD+PE+PF=8.
如图所示,△ABC是等边三角形,P是其内任意一点,PD∥AB,PE∥BC,PF∥AC,若△ABC的周长为24,则PD+PE+PF=8. 分析 可过点P作平行四边形PGBD,EPHC,进而利用平行四边形的性质及等边三角形的性质即可求解此题.
解答 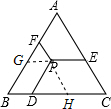 解:延长EP、FP分别交AB、BC于G、H,
解:延长EP、FP分别交AB、BC于G、H,
则由PD∥AB,PE∥BC,PF∥AC,可得,
四边形PGBD,EPHC是平行四边形,
∴PG=BD,PE=HC,
又∵△ABC是等边三角形,
又∵PF∥AC,PD∥AB,
∴△PFG,△PDH是等边三角形,
∴PF=PG=BD,PD=DH,
又∵△ABC的周长为24,
∴PD+PE+PF=DH+HC+BD=BC=$\frac{1}{3}$×24=8,
故答案为:8.
点评 本题主要考查了平行四边形的判定及性质以及等边三角形的判定及性质,应熟练掌握,解题的关键是得到△PFG,△PDH是等边三角形.


 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:初中数学 来源: 题型:解答题
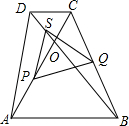 如图,在等腰梯形ABCD中,AB∥DC,AD=BC,对角线AC与BD相交于点O,∠ACD=60°,点S、P、Q分别为OD、OA、BC的中点.
如图,在等腰梯形ABCD中,AB∥DC,AD=BC,对角线AC与BD相交于点O,∠ACD=60°,点S、P、Q分别为OD、OA、BC的中点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
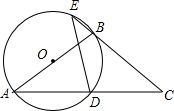 如图,点D是等腰△ABC底边的中点,过点A、B、D作⊙O.
如图,点D是等腰△ABC底边的中点,过点A、B、D作⊙O.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
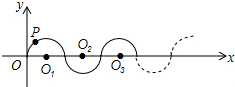 如图,在平面直角坐标系中,半径均为1各单位长度的半圆O1,O2,O3,…组成一条平滑的曲线,点P从原点O出发,沿这条曲线向右运动,速度为每秒$\frac{π}{2}$个单位长度,则第2015秒时,点P的坐标是(2015,-1).
如图,在平面直角坐标系中,半径均为1各单位长度的半圆O1,O2,O3,…组成一条平滑的曲线,点P从原点O出发,沿这条曲线向右运动,速度为每秒$\frac{π}{2}$个单位长度,则第2015秒时,点P的坐标是(2015,-1).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
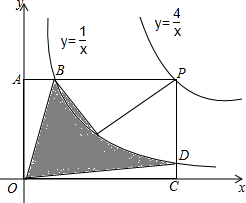 如图,点P为反比例函数y=$\frac{4}{x}$(x>0)图象上一点,过点P作y轴的垂线,交双曲线y=$\frac{1}{x}$于点B,交y轴于点A,过点P作x轴的垂线,交双曲线y=$\frac{1}{x}$于点D,交x轴于点C,连接OP交双曲线y=$\frac{1}{x}$于点E,则连接BO,OD,DE,EB而围成的阴影部分面积为( )
如图,点P为反比例函数y=$\frac{4}{x}$(x>0)图象上一点,过点P作y轴的垂线,交双曲线y=$\frac{1}{x}$于点B,交y轴于点A,过点P作x轴的垂线,交双曲线y=$\frac{1}{x}$于点D,交x轴于点C,连接OP交双曲线y=$\frac{1}{x}$于点E,则连接BO,OD,DE,EB而围成的阴影部分面积为( )| A. | 1 | B. | $\frac{5}{4}$ | C. | $\frac{4}{3}$ | D. | $\frac{3}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 在平面直角坐标系中,正方形ABCD的位置如图所示,点A的坐标为(1,0),点D的坐标为(0,2),延长CB交x轴于点A1,作正方形A1B1C1C;延长C1B1交x轴于点A2,作正方形A2B2C2C1;…,按这样的规律进行下去,第2016个正方形的面积为( )
在平面直角坐标系中,正方形ABCD的位置如图所示,点A的坐标为(1,0),点D的坐标为(0,2),延长CB交x轴于点A1,作正方形A1B1C1C;延长C1B1交x轴于点A2,作正方形A2B2C2C1;…,按这样的规律进行下去,第2016个正方形的面积为( )| A. | 5×($\frac{3}{2}$)2016 | B. | 5×($\frac{9}{4}$)2016 | C. | 5×($\frac{9}{4}$)2015 | D. | 5×($\frac{3}{2}$)4032 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知:如图,AB=AC,点D是BC的中点,AD=AE,AE⊥BE,垂足为E,连结DE.
已知:如图,AB=AC,点D是BC的中点,AD=AE,AE⊥BE,垂足为E,连结DE.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com