
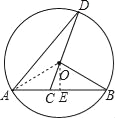
【题目】如图,已知AB是⊙O的弦,OB=2,∠B=30°,C是弦AB上任意一点(不与点A、B重合),连接CO并延长CO交⊙O于点D,连接AD.
(1)AB=_____;
(2)当∠D=20°时,求∠BOD的度数.
(3)若△ACD与△BCO相似,求AC的长.

【答案】(1)2![]() ;(2)100°;(3)
;(2)100°;(3)![]() .
.
【解析】试题分析:(1)过点O作OE⊥AB于E,由垂径定理即可求得AB的长;
(2)连接OA,由OA=OB,OA=OD,可得∠BAO=∠B,∠DAO=∠D,则可求得∠DAB的度数,又由圆周角等于同弧所对圆心角的一半,即可求得∠DOB的度数;
(3)由∠BCO=∠A+∠D,可得要使△ACD与△BCO相似,只能∠DCA=∠BCO=90°,然后由相似三角形的性质即可求得答案.
试题解析:解:(1)过点O作OE⊥AB于E,则AE=BE=![]() AB,∠OEB=90°.∵OB=2,∠B=30°,∴BE=OBcos∠B=2×
AB,∠OEB=90°.∵OB=2,∠B=30°,∴BE=OBcos∠B=2×![]() =
=![]() ,∴AB=
,∴AB=![]() .故答案为:
.故答案为: ![]() .
.
(2)连接OA.∵OA=OB,OA= OD,∴∠BAO=∠B,∠DAO=∠D,∴∠DAB=∠BAO+∠DAO=∠B+∠D.又∵∠B=30°,∠D=20°,∴∠DAB=50°,∴∠BOD=2∠DAB=100°;
(3)∵∠BCO=∠A+∠D,∴∠BCO>∠A,∠BCO>∠D,∴要使△ACD与△BCO相似,只能∠DCA=∠BCO=90°,此时∠BOC=60°,∠BOD=120°,∴∠DAC=60°,∴△DAC∽△BOC.∵∠BCO=90°,即OC⊥AB,∴AC= ![]() AB=
AB=![]() ,∴若△ACD与△BCO相似,AC的长度为
,∴若△ACD与△BCO相似,AC的长度为![]() .
.


 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案科目:初中数学 来源: 题型:
【题目】如图已知∠1与线段a,用直尺和圆规按下列步骤作图(保留作图痕迹,不写做法。)

(1)作等∠A于∠1
(2)在∠A的两边分别作AM=AN=a
(3)连接MN
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ACB和△DCE都是等腰直角三角形,CA=CB,CD=CE,∠ACB=∠DCE=90°,△ACB的顶点A在△DCE的斜边DE上,且AD=![]() ,AE=3
,AE=3![]() ,则AC=_____.
,则AC=_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料,解决后面三个问题:
我们可以将任意三位数表示为![]() (其中a、b、c分别表示百位上的数字,十位上的数字和个位上的数字,且a ≠0),显然
(其中a、b、c分别表示百位上的数字,十位上的数字和个位上的数字,且a ≠0),显然![]() =100a +10b +c;我们形如
=100a +10b +c;我们形如![]() 和
和![]() 的两个三位数称为一对“姊妹数”(其中x、y、z是三个连续的自然数)如:123和321是一对姊妹数,678和876是一对“姊妹数”。
的两个三位数称为一对“姊妹数”(其中x、y、z是三个连续的自然数)如:123和321是一对姊妹数,678和876是一对“姊妹数”。
(1)写出任意两对“姊妹数”。
(2)一对“姊妹数”的和为1110,求这对“姊妹数”。
(3)如果用x表示百位数字,求证:任意一对“姊妹数”的和能被37整除.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一张足够大的纸板上截取一个面积为3600平方厘米的矩形纸板ABCD,如图1,再在矩形纸板的四个角上切去边长相等的小正方形,再把它的边沿虚线折起,做成一个无盖的长方体纸盒,底面为矩形EFGH,如图2.设小正方形的边长为x厘米.
(1)当矩形纸板ABCD的一边长为90厘米时,求纸盒的侧面积的最大值;
(2)当EH:EF=7:2,且侧面积与底面积之比为9:7时,求x的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】足球训练中,为了训练球员快速抢断转身,教练设计了折返跑训练.教练在东西方向的足球场上画了一条直线插上不同的折返旗帜,如果约定向西为正,向东为负,练习一组的行驶记录如下(单位:米):+40,-30,+50,-25,+25,-30,+15,-28,+16,-20.
(1)球员最后到达的地方在出发点的哪个方向?距出发点多远?
(2)球员训练过程中,最远处离出发点多远?
(3)球员在一组练习过程中,跑了多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把矩形![]() 放入平面直角坐标系
放入平面直角坐标系![]() 中,使
中,使![]() 分别落在
分别落在![]() 轴的正半轴上,其中
轴的正半轴上,其中![]() ,对角线
,对角线![]() 所在直线解析式为
所在直线解析式为![]() ,将矩形
,将矩形![]() 沿着
沿着![]() 折叠,使点
折叠,使点![]() 落在边
落在边![]() 上的
上的![]() 处.
处.

(1)求点![]() 的坐标;
的坐标;
(2)求![]() 的长度;
的长度;
(3)点![]() 是
是![]() 轴上一动点,是否存在点
轴上一动点,是否存在点![]() 使得
使得![]() 的周长最小,若存在,请求出点
的周长最小,若存在,请求出点![]() 的坐标,如不存在,请说明理由.
的坐标,如不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】A、B两辆汽车同时从相距330千米的甲、乙两地相向而行,s(千米)表示汽车与甲地的距离,t(分)表示汽车行驶的时间,如图,L1,L2分别表示两辆汽车的s与t的关系.
(1)L1表示哪辆汽车到甲地的距离与行驶时间的关系?
(2)汽车B的速度是多少?
(3)求L1,L2分别表示的两辆汽车的s与t的关系式.
(4)2小时后,两车相距多少千米?
(5)行驶多长时间后,A、B两车相遇?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=![]() x2+mx+n与x轴相交于点A、B两点,过点B的直线y=x+b交抛物线于另一点C(-5,6),点D是线段BC上的一个动点(点D与点B、C不重合),作DE∥AC,交该抛物线于点E,
x2+mx+n与x轴相交于点A、B两点,过点B的直线y=x+b交抛物线于另一点C(-5,6),点D是线段BC上的一个动点(点D与点B、C不重合),作DE∥AC,交该抛物线于点E,
(1)求m,n,b的值;
(2)求tan∠ACB;
(3)探究在点D运动过程中,是否存在∠DEA=45°,若存在,则求此时线段AE的长;若不存在,请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com