

分析 (1)首先根据圆周角等于360°,求出的值是多少即可;然后用“视水价格调价涨幅抱无所谓态度”的居民的户数除以它占被调查的居民户数的分率,求出小明调查了多少户居民;最后求出每月每户的用水量在15m3-20m3之间的居民的户数,补全图1即可.
(2)根据中位数和众数的含义分别进行解答即可.
(3)根据分数乘法的意义,用小明所在小区居民的户数乘以“视调价涨幅采取相应的用水方式改变”的居民户数占被调查的居民户数的分率,求出“视调价涨幅采取相应的用水方式改变”的居民户数有多少即可.
解答 解:(1)n=360-120-30=210,
调查的居民户数为7÷$\frac{30°}{360°}$=84(户),
则每月每户的用水量在15m3-20m3之间的户数为84-(15+22+18+16+5)=8,
补全图1如下:
故答案为:210,84;
(2)∵共有84个数据,
∴每月每户用水量的中位数为第41、42个数据的平均数,即中位数落在15m3-20m3,
由条形图知,10m3-15m3的数据最多,
∴众数落在10m3-15m3,
故答案为:15m3-20m3,10m3-15m3;
(3)∵$1200×\frac{210}{360}=700$(户),
∴估计“视调价涨幅采取相应的用水方式改变”的居民户数有700户.
点评 此题主要考查了对条形统计图的认识和了解,要善于从条形统计图中获取信息,并能利用获取的信息解决实际问题.还考查了用样本估计总体,要熟练掌握,解答此题的关键是要明确众数、中位数、平均数、标准差与方差等的含义以及求法.


科目:初中数学 来源: 题型:填空题
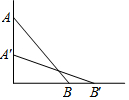 如图,一根长为a的竹竿AB斜靠在墙上,竹竿AB的倾斜角为α,当竹竿的顶端A下滑到点A'时,竹竿的另一端B向右滑到了点B',此时倾斜角为β.
如图,一根长为a的竹竿AB斜靠在墙上,竹竿AB的倾斜角为α,当竹竿的顶端A下滑到点A'时,竹竿的另一端B向右滑到了点B',此时倾斜角为β.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 已知Rt△DEF按如图所示的位置放置,∠E=90°,∠EDF=30°,DE=6$\sqrt{3}$,点H为线段FD延长线上一动点,现将△DEH绕点D顺时针旋转60°得到△DAK,E的对应点是A,H的对应点是K,若△EHK的面积为4$\sqrt{3}$,则DH的值为2.
已知Rt△DEF按如图所示的位置放置,∠E=90°,∠EDF=30°,DE=6$\sqrt{3}$,点H为线段FD延长线上一动点,现将△DEH绕点D顺时针旋转60°得到△DAK,E的对应点是A,H的对应点是K,若△EHK的面积为4$\sqrt{3}$,则DH的值为2.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
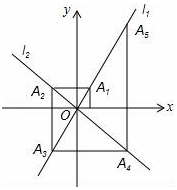 如图,在平面直角坐标系中,函数y=2x和y=-x的图象分别为直线l1,l2,过点(1,0)作x轴的垂线交l1于点A1,过点A1作y轴的垂线交l2于点A2,过点A2作x轴的垂线交l1于点A3,过点A3作y轴的垂线交l2于点A4,…依次进行下去,则点A2015的坐标为(-21007,-21008).
如图,在平面直角坐标系中,函数y=2x和y=-x的图象分别为直线l1,l2,过点(1,0)作x轴的垂线交l1于点A1,过点A1作y轴的垂线交l2于点A2,过点A2作x轴的垂线交l1于点A3,过点A3作y轴的垂线交l2于点A4,…依次进行下去,则点A2015的坐标为(-21007,-21008).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (2,3) | B. | (2,-3) | C. | (-2,3) | D. | (-2,-3) |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,甲、乙、丙、丁四个扇形的面积之比是1:2:3:4,则甲、乙、丙、丁四个扇形中圆心角度数最大的是( )度.
如图,甲、乙、丙、丁四个扇形的面积之比是1:2:3:4,则甲、乙、丙、丁四个扇形中圆心角度数最大的是( )度.| A. | 36 | B. | 72 | C. | 144 | D. | 156 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,已知函数y=-2x+4的图象,观察图象回答下列问题:
如图,已知函数y=-2x+4的图象,观察图象回答下列问题:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com