
【题目】研究问题:一个不透明的盒中装有若干个只有颜色不一样的红球与黄球,怎样估算不同颜色球的数量? 操作方法:先从盒中摸出8个球,画上记号放回盒中,再进行摸球实验,摸球实验的要求:先搅拌均匀,每次摸出一个球,放回盒中,再继续.
活动结果:摸球实验活动一共做了50次,统计结果如下表:
球的颜色 | 无记号 | 有记号 | ||
红色 | 黄色 | 红色 | 黄色 | |
摸到的次数 | 18 | 28 | 2 | 2 |
推测计算:由上述的摸球实验可推算:
(1)盒中红球、黄球各占总球数的百分比分别是多少?
(2)盒中有红球多少个?
科目:初中数学 来源: 题型:
【题目】小敏从A地出发向B地行走,同时小聪从B地出发向A地行走,如图所示,相交于点P的两条线段l1、l2分别表示小敏、小聪离B地的距离y(km)与已用时间x(h)之间的关系,则小敏、小聪行走的速度分别是( ) 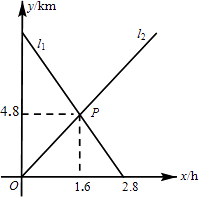
A.3km/h和4km/h
B.3km/h和3km/h
C.4km/h和4km/h
D.4km/h和3km/h
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,EF∥AD,∠1=∠2,∠BAC=70°.将求∠AGD的过程填写完整.

∵EF∥AD,( )
∴∠2= .(两直线平行,同位角相等)
又∵∠1=∠2,( )
∴∠1=∠3.( )
∴AB∥DG.( )
∴∠BAC+ =180°( )
又∵∠BAC=70°,( )
∴∠AGD= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一自助夏令营活动中,小明同学从营地A出发,要到A地的北偏东60°方向的C处,他先沿正东方向走了200m到达B地,再沿北偏东30°方向走,恰能到达目的地C(如图),那么,由此可知,B、C两地相距 m.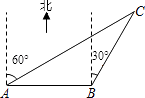
查看答案和解析>>
科目:初中数学 来源: 题型:
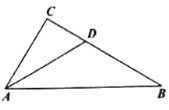
【题目】如图,∠CAB+∠ABC=90°,AD平分∠CAB,与BC边交于点D,BE平分∠ABC与AC边交于点E。
(1)依题意补全图形,并猜想∠DAB+∠EBA的度数等于__________;
(2)证明以上结论。
证明:∵ AD平分∠CAB,BE平分∠ABC,
∴∠DAB=![]() ∠CAB,
∠CAB,
∠EBA=__________.
(理由:____________________)
∵∠CAB+∠ABC=90°,
∴∠DAB+∠EBA=______×(∠______+∠______)=______。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知两直线l1 , l2分别经过点A(1,0),点B(﹣3,0),并且当两直线同时相交于y正半轴的点C时,恰好有l1⊥l2 , 经过点A、B、C的抛物线的对称轴与直线l1交于点K,如图所示.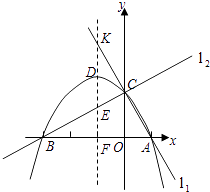
(1)求点C的坐标,并求出抛物线的函数解析式;
(2)抛物线的对称轴被直线l1 , 抛物线,直线l2和x轴依次截得三条线段,问这三条线段有何数量关系?请说明理由;
(3)当直线l2绕点C旋转时,与抛物线的另一个交点为M,请找出使△MCK为等腰三角形的点M,简述理由,并写出点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知函数y =(2m+1) x+ m-3
(1) 若函数图象经过原点,求m的值.
(2) 若函数图象在y轴的交点的纵坐标为-2,求m的值.
(3)若函数的图象平行直线y=-3x–3,求m的值.
(4)若这个函数是一次函数,且y随着x的增大而减小,求m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com