
科目:初中数学 来源: 题型:解答题
 为了发展乡村旅游,建设美丽从化,某中学七年级一班同学都积极参加了植树活动,今年四月份该班同学的植树情况部分如图所示,且植树2株的人数占32%.
为了发展乡村旅游,建设美丽从化,某中学七年级一班同学都积极参加了植树活动,今年四月份该班同学的植树情况部分如图所示,且植树2株的人数占32%.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
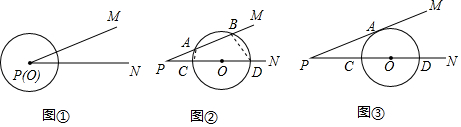
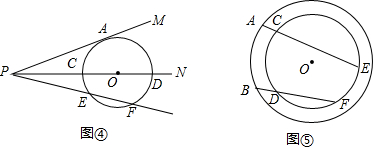
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
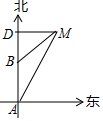 如图所示,轮船由A处以每小时28海里的速度向正北方向航行,此时测得灯塔M在北偏东30°的方向上(即∠BAM=30°).半小时后,轮船航行到B处,此时测得灯塔M在北偏东60°的方向(即∠DBM=60°).
如图所示,轮船由A处以每小时28海里的速度向正北方向航行,此时测得灯塔M在北偏东30°的方向上(即∠BAM=30°).半小时后,轮船航行到B处,此时测得灯塔M在北偏东60°的方向(即∠DBM=60°).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,某教学楼AB的后面有一建筑物CD,当光线与地面夹角是22°时,教学楼在建筑物的墙上留下高2米的影子CE;而当光线与地面夹角是45°时,教学楼顶A在地面上的影子F与墙角C有13米的距离(B、F、C在一条直线上),求教学楼AB的高度(sin22°≈$\frac{3}{8}$,cos22°≈$\frac{15}{16}$,tan22°≈$\frac{2}{5}$)
如图,某教学楼AB的后面有一建筑物CD,当光线与地面夹角是22°时,教学楼在建筑物的墙上留下高2米的影子CE;而当光线与地面夹角是45°时,教学楼顶A在地面上的影子F与墙角C有13米的距离(B、F、C在一条直线上),求教学楼AB的高度(sin22°≈$\frac{3}{8}$,cos22°≈$\frac{15}{16}$,tan22°≈$\frac{2}{5}$)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com