
分析 (1)根据题意可以得到多项式x4-y4分解侯的最终结果;
(2)根据题目中的数字和题意可以得到第三因式码;
(3)根据题意可以得到第一因式码一定是个位数,第二因式码是一位数或者两位数,第三因式码最大时三位数最小是一位数,从而可以估计出该题的答案.
解答 解:(1)x4-y4=(x2-y2)(x2+y2)=(x-y)(x+y)(x2+y2),
故答案为:x2+y2;
(2)∵x4-y4=(x-y)(x+y)(x2+y2),第一因式码和第二因式码构成“24”,
∴$\left\{\begin{array}{l}{x-y=2}\\{x+y=4}\end{array}\right.$,得$\left\{\begin{array}{l}{x=3}\\{y=1}\end{array}\right.$,
∴x2+y2=32+12=10,
∴第三因式码是10;
(3)由题意可得,
当x=9,y=5时,产生的密码最大,此时密码为414106.
点评 本题考查因式分解的应用,解答本题的关键是明确题意,找出所求问题需要的条件,利用因式分解的方法解答.


科目:初中数学 来源: 题型:选择题
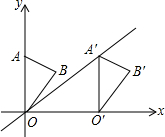 如图,在平面直角坐标系中,点A,B的坐标分别为(0,4)和(1,3)△OAB沿x轴向右平移后得到△O′A′B′,点A的对应点A′在直线y=$\frac{4}{5}$x上,则点B与O′间的距离为( )
如图,在平面直角坐标系中,点A,B的坐标分别为(0,4)和(1,3)△OAB沿x轴向右平移后得到△O′A′B′,点A的对应点A′在直线y=$\frac{4}{5}$x上,则点B与O′间的距离为( )| A. | 3 | B. | 4 | C. | 5 | D. | $\sqrt{34}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,AB是⊙O的直径,且AB=2cm,点P为弧AB上一动点(不与A,B重合),$\widehat{AD}$=$\widehat{BD}$,过点D作⊙O的切线交PB的延长线于点C.
如图,AB是⊙O的直径,且AB=2cm,点P为弧AB上一动点(不与A,B重合),$\widehat{AD}$=$\widehat{BD}$,过点D作⊙O的切线交PB的延长线于点C.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x=$\frac{1}{2}$ | B. | x=-$\frac{1}{2}$ | C. | x=2 | D. | x=-2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com