
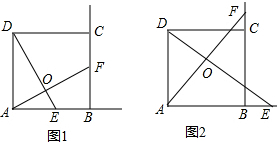
分析 (1)根据正方形的性质和全等三角形的判定定理证明△DAE≌△ABF,根据全等三角形的性质证明结论;
(2)①根据题意补全图形即可;
②想法1:根据平移的性质证明四边形FAEG是平行四边形,得到AF=EG,根据勾股定理得到DE2=AD2+AE2,证明△DAE≌△ABF,根据等腰直角三角形的性质解答;
想法2:延长AD、GF交于点H,证出∠H=90°,由勾股定理得出DG2=GH2+DH2,再证出DH=AE-AD,GH=AE+AD,即可得出结论.
解答 解:(1)∵四边形ABCD是正方形,
∴∠DAE=∠ABF=90°,DA=AB,
在△DAE和△ABF中,$\left\{\begin{array}{l}{DA=AB}&{\;}\\{∠DAE=∠ABF}&{\;}\\{AE=BF}&{\;}\end{array}\right.$,
∴△DAE≌△ABF(SAS),
∴DE=AF,∠ADE=∠BAF,
∵∠ADE+∠AED=90°,
∴∠BAF+∠AED=90°,即∠AOE=90°,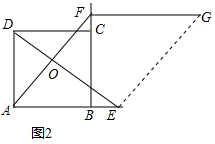
∴DE⊥AF,
故答案为:DE=AF;DE⊥AF;
(2)①补全图形如图所示:
②想法1::连接EG,如图2所示:
由题意得,AE=FG,AE∥FG,
∴四边形FAEG是平行四边形,
∴AF=EG,AF∥EG,
由勾股定理得,DE2=AD2+AE2,
在△DAE和△ABF中,$\left\{\begin{array}{l}{DA=AB}&{\;}\\{∠DAE=∠ABF}&{\;}\\{AE=BF}&{\;}\end{array}\right.$,
∴△DAE≌△ABF(SAS),
∴DE=AF,∠ADE=∠BAF,
∴DE=EG,
∵∠ADE+∠AED=90°,
∴∠BAF+∠AED=90°,即∠AOE=90°,
∴DE⊥AF,
∴DE⊥EG,
∴DG2=2DE2,
∴DG2=2AD2+2AE2.
想法2:延长AD、GF交于点H,如图3所示:
由平移的性质得:AE=FG,AE∥FG,
∵AD⊥AB,
∴GH⊥AD,四边形CDHF是矩形,
∴∠H=90°,HF=DC=AD,
∴DG2=GH2+DH2,
∵HG=FG+HF,
∴HG=AE+HF=AE+AD,
同①得:BF=AH,
∵BF=AE,
∴HD=AE-AD,
∴DG2=(AE+AD)2+(AE-AD)2=2AD2+2AE2.
点评 本题是四边形综合题目,考查的是正方形的性质、平移变换的性质、全等三角形的判定和性质、等腰直角三角形的性质、勾股定理、矩形的性质完全平方公式等知识;本题综合性强,有一定难度,证明三角形全等是解决问题的关键.


 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案科目:初中数学 来源: 题型:解答题
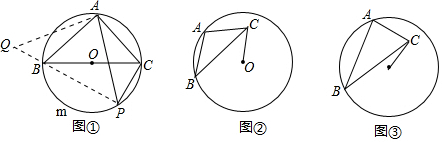
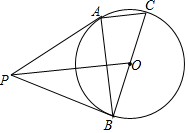 如图,P为⊙O外一点,BC是⊙O的直径,CA为⊙O的一条弦,连接PA、PB,∠PBA=∠C.
如图,P为⊙O外一点,BC是⊙O的直径,CA为⊙O的一条弦,连接PA、PB,∠PBA=∠C.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
| 苹果总质量n(kg) | 100 | 200 | 300 | 400 | 500 | 1000 |
| 损坏苹果质量m(kg) | 10.50 | 19.42 | 30.63 | 39.24 | 49.54 | 101.10 |
| 苹果损坏的频率$\frac{m}{n}$(结果保留小数点后三位) | 0.105 | 0.097 | 0.102 | 0.098 | 0.099 | 0.101 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
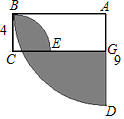 以A为圆心,半径为9的四分之一圆,与以C为圆心,半径为4的四分之一圆如图所示放置,且∠ABC=90°,则图中阴影部分的面积为$\frac{97}{4}$π-36.
以A为圆心,半径为9的四分之一圆,与以C为圆心,半径为4的四分之一圆如图所示放置,且∠ABC=90°,则图中阴影部分的面积为$\frac{97}{4}$π-36.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
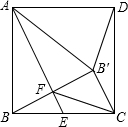 在正方形ABCD中,点E为BC边的中点,把△ABE沿直线AE折叠,B点落在点B′处,B′B与AE交于点F,连接AB′,DB′,FC.下列结论:①AB′=AD;②△FCB′为等腰直角三角形;③∠CB′D=135°;④BB′=BC;⑤AB2=AE•AF.其中正确的个数为( )
在正方形ABCD中,点E为BC边的中点,把△ABE沿直线AE折叠,B点落在点B′处,B′B与AE交于点F,连接AB′,DB′,FC.下列结论:①AB′=AD;②△FCB′为等腰直角三角形;③∠CB′D=135°;④BB′=BC;⑤AB2=AE•AF.其中正确的个数为( )| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 7.65×108 | B. | 76.5×107 | C. | 0.765×109 | D. | 765×106 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com