
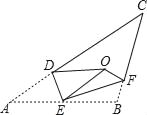
【题目】如图,将△ABC沿DE、EF翻折,顶点A,B均落在点O处,且EA与EB重合于线段EO,若∠CDO+∠CFO=100°,则∠C的度数为( )
A. 40° B. 41° C. 42° D. 43°
【答案】A
【解析】
连接AO、BO.由题意知:EA=EB=EO,推出∠AOB=90°,∠OAB+∠OBA=90°,由DO=DA,FO=FB,推出∠DAO=∠DOA,∠FOB=∠FBO,推出∠CDO=2∠DAO,∠CFO=2∠FBO,由∠CDO+∠CFO=100°,推出∠DAO+∠FBO=50°,由此即可解决问题.
如图,连接AO、BO.
由题意知:EA=EB=EO,∴∠AOB=90°,∠OAB+∠OBA=90°.
∵DO=DA,FO=FB,∴∠DAO=∠DOA,∠FOB=∠FBO,∴∠CDO=2∠DAO,∠CFO=2∠FBO.
∵∠CDO+∠CFO=100°,∴2∠DAO+2∠FBO=100°,∴∠DAO+∠FBO=50°,∴∠CAB+∠CBA=∠DAO+∠OAB+∠OBA+∠FBO=140°,∴∠C=180°﹣(∠CAB+∠CBA)=180°﹣140°=40°.
故选A.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,边长分别为2和4的两个全等三角形,开始它们在左边重叠,大△ABC固定不动,然后把小△A′B′C′自左向右平移,直至移到点B′到C重合时停止,设小三角形移动的距离为x,两个三角形的重合部分的面积为y,则y关于x的函数图象是( )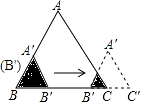
A.
B.
C.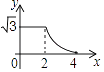
D.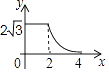
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AD∥BC,∠ABC+∠DCB=90°,且BC=2AD,分别以AB、BC、DC为边向外作正方形,它们的面积分别为S1、S2、S3.若S2=48,S3=9,则S1的值为( )
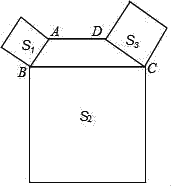
A. 18 B. 12 C. 9 D. 3
查看答案和解析>>
科目:初中数学 来源: 题型:
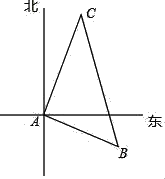
【题目】如图,有一艘货船和一艘客船同时从港口A出发,客船每小时比货船多走5海里,客船与货船速度的比为4:3,货船沿东偏南10°方向航行,2小时后货船到达B处,客船到达C处,若此时两船相距50海里.
(1)求两船的速度分别是多少?
(2)求客船航行的方向.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明在学习过程中,对教材中的一个有趣问题做如下探究:
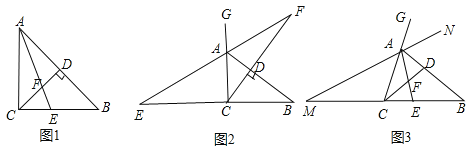
(习题回顾)已知:如图1,在△ABC中,∠ACB=90°,AE是角平分线,CD是高,AE、CD相交于点F.求证:∠CFE=∠CEF;
(变式思考)如图2,在△ABC中,∠ACB=90°,CD是AB边上的高,若△ABC的外角∠BAG的平分线交CD的延长线于点F,其反向延长线与BC边的延长线交于点E,则∠CFE与∠CEF还相等吗?说明理由;
(探究廷伸)如图3,在△ABC中,在AB上存在一点D,使得∠ACD=∠B,角平分线AE交CD于点F.△ABC的外角∠BAG的平分线所在直线MN与BC的延长线交于点M.试判断∠M与∠CFE的数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠B=30°,∠ACB=90°,CD⊥AB交AB于D,以CD为较短的直角边向△CDB的同侧作Rt△DEC,满足∠E=30°,∠DCE=90°,再用同样的方法作Rt△FGC,∠FCG=90°,继续用同样的方法作Rt△HIC,∠HCI=90°.若AC=a,求CI的长.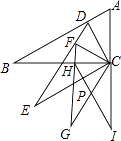
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】试找出如图所示的每个正多边形的对称轴的条数,并填入表格中.
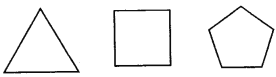
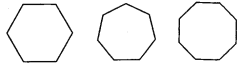
正多边形的边数 | 3 | 4 | 5 | 6 | 7 | 8 |
对称轴的条数 |
根据上表,请就一个正n边形对称轴的条数作一猜想.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com