
【题目】如图,已知在矩形ABCD中,AB=a,BC=b,点E是线段AD边上的任意一点(不含端点A、D),连结BE、CE.
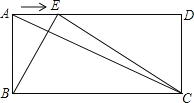
(1)若a=5,sin∠ACB=![]() ,求b.
,求b.
(2)若a=5,b=10当BE⊥AC时,求出此时AE的长.
(3)设AE=x,试探索点E在线段AD上运动过程中,使得△ABE与△BCE相似时,求a、b应满足什么条件,并求出此时x的值.
【答案】(1)b=12;(2)![]() ;(3)当a、b满足条件b=2a时△BAE∽△CEB,此时
;(3)当a、b满足条件b=2a时△BAE∽△CEB,此时![]() (或x=a);当a、b满足条件b>2a时△BAE∽△CEB,此时
(或x=a);当a、b满足条件b>2a时△BAE∽△CEB,此时![]() .
.
【解析】
试题分析:(1)①在矩形ABCD中,得到∠ABC=90°,解直角三角形即可得到结果;
(2)由BE⊥A,得到∠2+∠3=90°,由于∠1+∠3=90°,等量代换得到∠1=∠2,推出△AEB∽△BAC,得到比例式,即可得到结论;
(3)点E在线段AD上的任一点,且不与A、D重合,当△ABE与△BCE相似时,则∠BEC=90°当△BAE∽△CEB(如图2),∠1=∠BCE,又BC∥AD,由平行线的性质得到∠2=∠BCE,推出△BAE∽△EDC,得到比例式,进而可得得到一元二次方程x2﹣bx+a2=0,根据方程根的情况,得到结论.
解:(1)
∵四边形ABCD是矩形,
∴∠ABC=90°,
∵AB=a=5,sin∠ACB=![]() ,
,
∴![]() ,
,
∴AC=13,
∴BC=![]() =12,
=12,
∴b=12;
(2)如图1,
∵BE⊥AC,
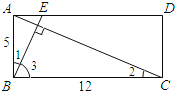
∴∠2+∠3=90°,
又∠1+∠3=90°,
∴∠1=∠2,
又∠BAE=∠ABC=90°,
∴△AEB∽△BAC,
∴![]() ,
,
即![]() ,
,
∴![]() ;
;
(3)∵点E在线段AD上的任一点,且不与A、D重合,
∴当△ABE与△BCE相似时,则∠BEC=90°
所以当△BAE∽△CEB(如图2)
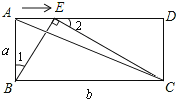
则∠1=∠BCE,
又BC∥AD,
∴∠2=∠BCE,
∴∠1=∠2,
又∠BAE=∠EDC=90°,
∴△BAE∽△EDC,
∴![]() ,
,
即![]() ,
,
∴x2﹣bx+a2=0,
即![]() ,
,
当b2﹣4a2≥0,
∵a>0,b>0,
∴b≥2a,
即b≥2a时,![]() ,
,
综上所述:当a、b满足条件b=2a时△BAE∽△CEB,此时![]() (或x=a);
(或x=a);
当a、b满足条件b>2a时△BAE∽△CEB,此时![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,某市对位于笔直公路上的两个小区A、B的供水路线进行优化改造,测得供水站M在小区A的南偏东60°方向,在小区B的西南方向,小区B到供水站M的距离为300米,
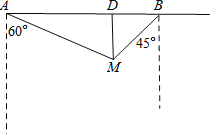
(1)求供水站M到公路AB的垂直距离MD的长度.
(2)求小区A到供水站M的距离.(结果可保留根号)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com