
| A. |  | B. |  | C. | 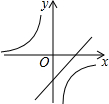 | D. | 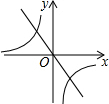 |
分析 先根据一次函数的性质判断出m取值,再根据反比例函数的性质判断出m的取值,二者一致的即为正确答案.
解答 解:A、由y=nx+m(n>0)图象可知n>0,m=0,由$y=\frac{n}{x+m}$的图象可知n>0,m=0,故A正确;
B、由y=nx+m(n>0)图象可知n<0,m=0,由$y=\frac{n}{x+m}$的图象可知n>0,m=0,相矛盾,故B错误;
C、由y=nx+m(n>0)图象可知n>0,m<0,由$y=\frac{n}{x+m}$的图象可知n<0,m=0,相矛盾,故C错误;
D、由y=nx+m(n>0)图象可知n<0,m=0,由$y=\frac{n}{x+m}$的图象可知n<0,m=0,与已知矛盾,故D错误;
故选:A.
点评 本题主要考查了反比例函数的图象性质和一次函数的图象性质,要掌握它们的性质才能灵活解题.


科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
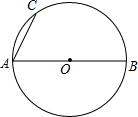 如图,AB是⊙O的直径,AC为弦.
如图,AB是⊙O的直径,AC为弦.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某学校准备组织八年级学生春游,供学生选择的春游地点分别是:植物园、太阳岛、东北虎林园.每名学生只能选择其中一个春游地点(必选且只选一个).该校从八年级学生中随机抽取了a名学生,对他们选择春游地点的情况进行调查,并根据调查结果绘制成如图所示的条形统计图.
某学校准备组织八年级学生春游,供学生选择的春游地点分别是:植物园、太阳岛、东北虎林园.每名学生只能选择其中一个春游地点(必选且只选一个).该校从八年级学生中随机抽取了a名学生,对他们选择春游地点的情况进行调查,并根据调查结果绘制成如图所示的条形统计图.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某单位准备印制一批证书,现有两个印刷厂可供选择,甲厂费用分为制版费和印刷费两部分先收取固定的制版费,再按印刷数量收取印刷费,
某单位准备印制一批证书,现有两个印刷厂可供选择,甲厂费用分为制版费和印刷费两部分先收取固定的制版费,再按印刷数量收取印刷费,查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在⊙O中,MN是直径,AB是弦,且MN⊥AB,垂足为C,下列结论:
如图,在⊙O中,MN是直径,AB是弦,且MN⊥AB,垂足为C,下列结论:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在△ABE中,点C在AE上,AB=AC=5,∠CBE=$\frac{1}{2}$∠A,sin∠CBE=$\frac{\sqrt{5}}{5}$,求BC和BE的长.
如图,在△ABE中,点C在AE上,AB=AC=5,∠CBE=$\frac{1}{2}$∠A,sin∠CBE=$\frac{\sqrt{5}}{5}$,求BC和BE的长.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com