
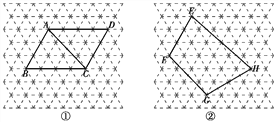
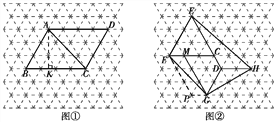
【题目】图中的虚线网格是等边三角形网格,它的每一个小三角形都是边长为1的等边三角形.
(1)边长为1的等边三角形的高=____;
(2)图①中的ABCD的对角线AC的长=____;
(3)图②中的四边形EFGH的面积=____.
【答案】 ![]()
![]() 8
8![]()
【解析】分析:(1)利用等边三角形的性质和勾股定理求出高;
(2)要求AC的长,构造直角三角形,应用勾股定理求出.
(3)要求四边形EFGH的面积,先将其分割,然后求每部分的面积,再相加和即可.
详解:(1)边长为1的等边三角形的高=![]() =
=![]() .
.
(2)过点A作AK⊥BC于K(如图①),
由图①知,ABCD的面积等于24个小等边三角形的面积和,由(1)知每个小等边三角形的面积为![]() ×1×
×1×![]() =
=![]() ,∴SABCD=24×
,∴SABCD=24×![]() =6
=6![]() .又SABCD=BC·AK,BC=4,∴AK=6
.又SABCD=BC·AK,BC=4,∴AK=6![]() ÷4=
÷4=![]() ,又在Rt△ABK中,AB=3,∴BK=
,又在Rt△ABK中,AB=3,∴BK=![]() =
=![]() ,∴KC=
,∴KC=![]() ,
,
∴AC=![]() =
=![]() .
.
(3)如图②所示,将四边形EFGH分割成五部分,以FG为对角线构造FPGM,
∵FPGM含有6个小等边三角形,
∴S△FGM=3S小等边三角形,
同理可得S△DGH=4S小等边三角形,S△EFC=9S小等边三角形,S△EDH=8S小等边三角形,又S四边形CMGD=8S小等边三角形,
由(2)知小等边三角形的面积为![]() ,
,
∴S四边形EFGH=(3+4+9+8+8)×![]() =8
=8![]() .
.


科目:初中数学 来源: 题型:
【题目】生态公园计划在园内的坡地上种植一片有A、B两种树的混合林,需要购买这两种树苗共100棵.假设这批树苗种植后成活95棵,种植A、B两种树苗的相关信息如下表:

(1)求购买这两种树苗各多少棵?
(2)求种植这片混合林的总费用需多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知正比例函数y=k1x的图象与反比例函数y= ![]() 的图象的一个交点是(2,3).
的图象的一个交点是(2,3).
(1)求出这两个函数的表达式;
(2)作出两个函数的草图,利用你所作的图形,猜想并验证这两个函数图象的另一个交点的坐标;
(3)直接写出使反比例函数值大于正比例函数值的x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
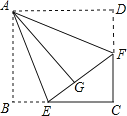
【题目】如图,正方形纸片ABCD的边长为3,点E、F分别在边BC、CD上,将AB、AD分别沿AE、AF折叠,点B、D恰好都落在点G处,已知BE=1,求EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣x2+bx+c与x轴交于点A(﹣1,0),B(5,0)两点,直线y=﹣ ![]() x+3与y轴交于点C,与x轴交于点D.点P是x轴上方的抛物线上一动点,过点P作PF⊥x轴于点F,交直线CD于点E.设点P的横坐标为m.
x+3与y轴交于点C,与x轴交于点D.点P是x轴上方的抛物线上一动点,过点P作PF⊥x轴于点F,交直线CD于点E.设点P的横坐标为m.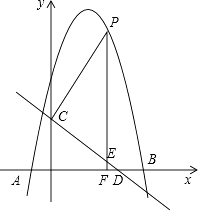
(1)求抛物线的解析式;
(2)若PE=5EF,求m的值;
(3)若点E′是点E关于直线PC的对称点,是否存在点P,使点E′落在y轴上?若存在,请直接写出相应的点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2016年春季,建阳区某服装商店分两次从批发市场购进同一款服装,数量之比是2:3,且第一、二次进货价分别为每件50元、40元,总共付了4400元的货款.
(1)求第一、二次购进服装的数量分别是多少件?
(2)由于该款服装刚推出时,很受欢迎,按每件70元销售了x件;后来,由于该服装滞销,为了及时处理库存,缓解资金压力,其剩余部分的按每件30元全部售完.当x的值至少为多少时,该服装商店才不会亏本.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校测量了九年级(1)班学生的身高(精确到1cm),按10cm为一段进行分组,得到如下频数分布直方图如图,则下列说法不正确的是( )

A. 该班人数最多的身高段的学生数为20人
B. 该班身高低于160.5 cm的学生数为20人
C. 该班身高最高段的学生数为20人
D. 该班身高最高段的学生数为7人
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)写出方程 x + y =3的两个解__________,把方程 x + y =3化成一次函数的形式为__________;
(2)以方程 x + y =3的解为坐标的所有点组成的图象与一次函数 y =3- x 的图象相同吗?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com