
【题目】如图,平面直角坐标系中,点A1的坐标为(1,2),以O为圆心,OA1长为半径画弧,交直线y=![]() x于点B1.过点B1作B1A2∥y轴交直线y=2x于点A2,以O为圆心,OA2长为半径画弧,交直线y═
x于点B1.过点B1作B1A2∥y轴交直线y=2x于点A2,以O为圆心,OA2长为半径画弧,交直线y═![]() x于点B2;过点B2作B2A3∥y轴交直线y=2x于点A3,以点O为圆心,OA3长为半径画弧,交直线y=
x于点B2;过点B2作B2A3∥y轴交直线y=2x于点A3,以点O为圆心,OA3长为半径画弧,交直线y=![]() x于点B3;……按如此规律进行下去,点B2020的坐标为_____.
x于点B3;……按如此规律进行下去,点B2020的坐标为_____.

科目:初中数学 来源: 题型:
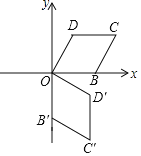
【题目】如图,在菱形OBCD中,OB=1,相邻两内角之比为1:2,将菱形OBCD绕顶点O顺时针旋转90°,得到菱形OB′C′D′视为一次旋转,则菱形旋转45次后点C的坐标为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线G:![]() 有最低点。
有最低点。
(1)求二次函数![]() 的最小值(用含m的式子表示);
的最小值(用含m的式子表示);
(2)将抛物线G向右平移m个单位得到抛物线G1。经过探究发现,随着m的变化,抛物线G1顶点的纵坐标y与横坐标x之间存在一个函数关系,求这个函数关系式,并写出自变量x的取值范围;
(3)记(2)所求的函数为H,抛物线G与函数H的图像交于点P,结合图像,求点P的纵坐标的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,直线y=x+2经过点A(m,-2),将点A向右平移7个单位长度,得到点B,抛物线![]() 的顶点为C.
的顶点为C.
(1)求m的值和点B的坐标;
(2)求点C的坐标(用含n的代数式表示);
(3)若抛物线与线段AB只有一个公共点,结合函数图象,求n的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
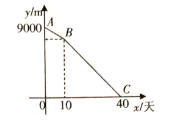
【题目】某街道需要铺设管线的总长为9000![]() ,计划由甲队施工,每天完成150
,计划由甲队施工,每天完成150![]() .工作一段时间后,因为天气原因,想要40天完工,所以增加了乙队.如图表示剩余管线的长度
.工作一段时间后,因为天气原因,想要40天完工,所以增加了乙队.如图表示剩余管线的长度![]() 与甲队工作时间
与甲队工作时间![]() (天)之间的函数关系图象.
(天)之间的函数关系图象.
(1)直接写出点![]() 的坐标;
的坐标;
(2)求线段![]() 所对应的函数解析式,并写出自变量
所对应的函数解析式,并写出自变量![]() 的取值范围;
的取值范围;
(3)直接写出乙队工作25天后剩余管线的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
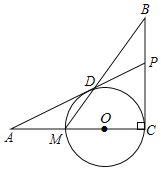
【题目】如图,已知BC⊥AC,圆心O在AC上,点M与点C分别是AC与⊙O的交点,点D是MB与⊙O的交点,点P是AD延长线与BC的交点,且ADAO=AMAP.
(1)连接OP,证明:△ADM∽△APO;
(2)证明:PD是⊙O的切线;
(3)若AD=12,AM=MC,求PB和DM的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有若干个仅颜色不同的红球和黑球,现往一个不透明的袋子里装进2个红球和3个黑球.
(1)随机摸出一个球是黑球的概率为 ;若先从袋子里取出m个红球(不放回),再从袋子里随机摸出一个球,将“摸到黑球”记为事件A.若事件A为必然事件,则m= ;
(2)若先从袋子里摸出一个球,放回后再摸出一个球,用列表法或画树状图法求出两次摸出的球颜色不同的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某年五月,我国南方某省A、B两市遭受严重洪涝灾害,邻近县市C、D决定调运物资支援A、B两市灾区.已知C市有救灾物资240吨,D市有救灾物资260吨,现将这些救灾物资全部调往A、B两市,A市需要的物资比B市需要的物资少100吨.已知从C市运往A、B两市的费用分别为每吨20元和25元,从D市运往往A、B两市的费用分别为每吨15元和30元,设从D市运往B市的救灾物资为x吨.
(1)A、B两市各需救灾物资多少吨?
(2)设C、D两市的总运费为w元,求w与x之间的函数关系式,并写出自变量x的取值范围;
(3)经过抢修,从D市到B市的路况得到了改善,缩短了运输时间,运费每吨减少m元(m>0),其余路线运费不变.若C、D两市的总运费的最小值不小于10320元,求m的取值范围.
查看答案和解析>>
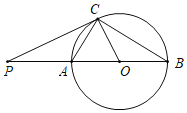
科目:初中数学 来源: 题型:
【题目】如图,已知AB是⊙O的直径,AC是弦,点P是BA延长线上一点,连接PC、BC,∠PCA=∠B.
(1)求证:PC是⊙O的切线;
(2)若PC=4,PA=2,求直径AB的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com