
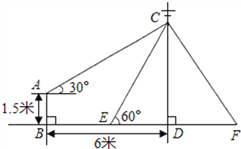
【题目】如图,在电线杆上的C处引拉线CE、CF固定电线杆,拉线CE和地面所成的角
∠CED=60°,在离电线杆6米的B处安置测角仪AB,在A处测得电线杆上C处的仰角为30°,已知测角仪高AB为1.5米,求拉线CE的长 (结果精确到0.1米,参考数据:![]() ≈1.414,
≈1.414,![]() ≈1.732).
≈1.732).
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案科目:初中数学 来源: 题型:
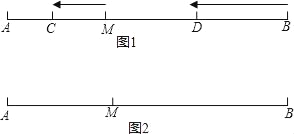
【题目】如图①,已知点M是线段AB上一点,点C在线段AM上,点D在线段BM上,C、D两点分别从M、B出发以1cm/s、3cm/s的速度沿直线BA向左运动,运动方向如箭头所示.
(1)若AB=10cm,当点C、D运动了2s,求AC+MD的值.
(2)若点C、D运动时,总有MD=3AC,则:AM= AB.
(3)如图②,若AM=![]() AB,点N是直线AB上一点,且AN﹣BN=MN,求
AB,点N是直线AB上一点,且AN﹣BN=MN,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,O是正△ABC内一点,OA=3,OB=4,OC=5,将线段BO以点B为旋转中心逆时针旋转60°得到线段BO′,下列结论:①△BO′A可以由△BOC绕点B逆时针旋转60°得到;②点O与O′的距离为4;③∠AOB=150°;④S四边形AOBO![]() ;⑤S△AOC+S△AOB=
;⑤S△AOC+S△AOB=![]() .其中正确的结论是( )
.其中正确的结论是( )
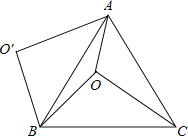
A.①②③⑤B.①②③④C.①②③④⑤D.①②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面一段文字:
在数轴上点A,B分别表示数a,b.A,B两点间的距离可以用符号![]() 表示,利用有理数减法和绝对值可以计算A,B两点之间的距离
表示,利用有理数减法和绝对值可以计算A,B两点之间的距离![]() .
.
例如:当a=2,b=5时,![]() =5-2=3;当a=2,b=-5时,
=5-2=3;当a=2,b=-5时,![]() =
=![]() =7;当a=-2,b=-5时,
=7;当a=-2,b=-5时,![]() =
=![]() =3.综合上述过程,发现点A、B之间的距离
=3.综合上述过程,发现点A、B之间的距离![]() =
=![]() (也可以表示为
(也可以表示为![]() ).
).
请你根据上述材料,探究回答下列问题:
(1)数轴上表示1和3两点之间的距离是 ;
(2)表示数a和-2的两点间距离是6,则a= ;
(3)如果数轴上表示数a的点位于-4和3之间,求![]() 的值.
的值.
(4)是否存在数a,使代数式![]() 的值最小?若存在,请求出代数式的最小值,并直接写出数a的值或取值范围,若不存在,请简要说明理由.
的值最小?若存在,请求出代数式的最小值,并直接写出数a的值或取值范围,若不存在,请简要说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】设(a,b)是一次函数y=(k-2)x+m与反比例函数![]() 的图象的交点,且a、b是关于x的一元二次方程
的图象的交点,且a、b是关于x的一元二次方程![]() 的两个不相等的实数根,其中k为非负整数,m、n为常数.
的两个不相等的实数根,其中k为非负整数,m、n为常数.
(1)求k的值;
(2)求一次函数与反比例函数的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】油箱中有油30kg,油从管道中匀速流出,1小时流完,求油箱中剩余油量Q(kg)与流出时间t(分钟)间的函数关系式为__________________,自变量的范围是_____________.当Q=10kg时,t=_______________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=k1x+b与反比例函数y=![]() 的图象交于点A(m,2),B(2,-1).
的图象交于点A(m,2),B(2,-1).
(1)求这两个函数的表达式;
(2)在x轴上是否存在点P(n,0),使△ABP为直角三角形,请你直接写出P点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
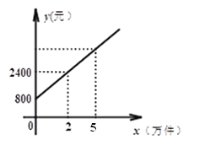
【题目】某公司市场营销部的某营销员的个人月收入与该营销员每月的销售量成一次函数关系,其图像如图所示.根据图像提供的信息,解答下列问题:
(1)求营销员的个人月收入y元与该营销员每月的销售量x万件(x≥0)之间的函数关系式;
(2)若两个月内该营销员的销售量从2万件猛增到5万件,月收入两个月大幅度增长,且连续两个月的月收入的增长率是相同的,试求这个增长率(![]() ,保留到百分位).
,保留到百分位).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com