
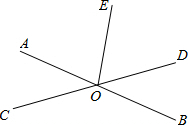
 如图,直线AB、CD相交于点O,OE平分∠AOD.
如图,直线AB、CD相交于点O,OE平分∠AOD.分析 (1)根据题意可知,∠AOC+∠AOD=180°,求得∠AOD,然后再由OE平分∠AOD,得出∠DOE=∠AOE,从而可以求出∠DOE的度数;
(2)由(1)知∠DOE=$\frac{1}{2}$∠AOD=90°-$\frac{1}{2}$x,根据对顶角定理有∠BOD=x,则∠BOE=∠BOD+∠DOE代入即可.
解答 解:(1)∵∠AOC=46°,
∴∠AOD=180°-∠AOC=134°,
又∵OE平分∠AOD,
∴∠DOE=$\frac{1}{2}$∠AOD,
∴∠DOE=72°;
(2))∵∠AOC=x,
∴∠AOD=180°-∠AOC=180°-x,∠BOD=x,
又∵OE平分∠AOD,
∴∠DOE=$\frac{1}{2}$∠AOD=90°-$\frac{1}{2}$x,
∴∠BOE=∠BOD+∠DOE=90°+$\frac{1}{2}$x.
点评 本题考查了对顶角和邻补角,以及角平分线的定义,解题的关键是熟练运用定义,此题比较简单,易于掌握.


科目:初中数学 来源: 题型:选择题
 如图,直线y=kx+b与y轴交于点(0,3),与X轴交于点(a,0),当-3≤a<0时,k的取值范围( )
如图,直线y=kx+b与y轴交于点(0,3),与X轴交于点(a,0),当-3≤a<0时,k的取值范围( )| A. | -1≤k<0 | B. | k≥1 | C. | 1≤k≤3 | D. | k≥3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
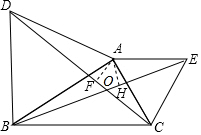 如图,已知△ABD,△AEC都是等边三角形,AF⊥CD于F,AH⊥BE于H,问:
如图,已知△ABD,△AEC都是等边三角形,AF⊥CD于F,AH⊥BE于H,问:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源:2016-2017学年江苏省苏州太仓市第二学期初一期中模拟数学试卷(解析版) 题型:单选题
若(x+y)2=9,(x﹣y)2=5,则xy的值为( )
A. ﹣1; B. 1 ; C. ﹣4; D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com