练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    8．绝对值大于1而不大于4的负整数有-2、-3、-4．

    分析 首先判断出绝对值大于1而不大于4的负整数的绝对值等于2、3、4，然后根据绝对值的大小，判断出绝对值大于1而不大于4的负整数有哪些即可．

    解答 解：∵绝对值大于1而不大于4的负整数的绝对值等于2、3、4，
    ∴绝对值大于1而不大于4的负整数有-2、-3、-4．
    故答案为：-2、-3、-4．

    点评 （1）此题主要考查了有理数大小比较的方法，要熟练掌握，解答此题的关键是要明确：①正数都大于0；②负数都小于0；③正数大于一切负数；④两个负数，绝对值大的其值反而小．
    （2）此题还考查了绝对值的含义和应用，要熟练掌握，解答此题的关键是要明确：①当a是正有理数时，a的绝对值是它本身a；②当a是负有理数时，a的绝对值是它的相反数-a；③当a是零时，a的绝对值是零．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    18．已知点O是△ABC内任意一点，连接OA并延长到E，使得AE=OA，以OB，OC为邻边作?OBFC，连接OF与BC交于点H，再连接EF．
    （1）如图1，若△ABC为等边三角形，求证：①EF⊥BC；②EF=$\sqrt{3}$BC；
    （2）如图2，若△ABC为等腰直角三角形（BC为斜边），猜想（1）中的两个结论是否成立？若成立，直接写出结论即可；若不成立，请你直接写出你的猜想结果；
    （3）如图3，若△ABC是等腰三角形，且AB=AC=kBC，请你直接写出EF与BC之间的数量关系．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

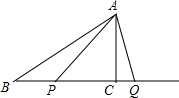    19．如图，Rt△ABC中，∠ACB=90°，BC=4cm，AC=acm，动点P，Q分别从点B，点C开始沿着射线BC运动，点P的速度为2cm/s，点Q的速度为1cm/s．两点同时出发，当点P追上点Q时两点都停止运动，设运动时间为t秒．
    （1）若a=2cm
    ①求两点都停止运动时，△ABQ的面积．
    ②是否存在t，使得△APQ为等腰三角形？若存在，请求出t的值；若不存在，请说明理由；
    （2）若刚好存在某一时刻t，使得AP，AC三等分∠BAQ，则a的值为$\frac{2\sqrt{3}}{3}$（直接写出答案）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    16．如图，△ABC中，AD⊥BC于D，若AB=15，AC=13，BC=14，求AD．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    3．抛物线y=-x2+2kx+2与x轴的交点个数为（　　）
    A．0个B．1个C．2个D．3个

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    13．计算下列各题：
    （1）$\frac{1}{2}{a^2}b{c^3}•{（-2{a^2}{b^2}c）^2}$
    （2）（25m2+15m3n-20m4）÷（-5m2）
    （3）（2a+3b）（2a-3b）-（a-3b）2
    （4）化简求值 （x+2y）2-（x+y）（x-y），其中$x=-2，y=\frac{1}{2}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    20．学校为了考察我校八年级同学的视力情况，从八年级的17个班共850名学生中，每班抽取了5名进行分析．在这个问题中．样本是85名学生的视力情况，样本的容量是85．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    17．下列计算正确的是（　　）
    A．3$\sqrt{2}$×4$\sqrt{2}$=12$\sqrt{2}$B．$\sqrt{（-9）×（-25）}=\sqrt{9}×\sqrt{-25}=（-3）×（-5）=15$
    C．-3$\sqrt{\frac{2}{3}}$=$\sqrt{{{（-3）}^2}×\frac{2}{3}}$=6D．$\sqrt{{{13}^2}-{{12}^2}}=\sqrt{（13+12）（13-12）}$=5

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    18．若$\frac{a}{3}$+1与$\frac{2a+1}{3}$的绝对值相等，则a的值为（　　）
    A．2B．$\frac{4}{3}$C．2或$\frac{4}{3}$D．2或-$\frac{4}{3}$

    查看答案和解析>>

    同步练习册答案