
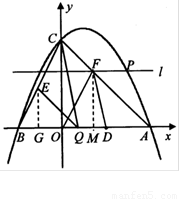
(本题12分)已知:如图,二次函数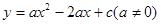 的图象与y轴交于点C(0,4),与x轴交于点A、B,点A的坐标为(4,0).
的图象与y轴交于点C(0,4),与x轴交于点A、B,点A的坐标为(4,0).
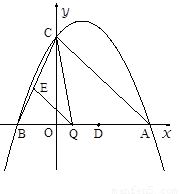
1.(1)求该二次函数的关系式;
2.(2)写出该二次函数的对称轴和顶点坐标;
3.(3)点Q是线段AB上的动点,过点Q作QE∥AC,交BC于点E,连接CQ.当△CQE的面积最大时,求点Q的坐标;
4.(4)若平行于x轴的动直线 与该抛物线交于点P,与直线AC交于点F,点D的坐标为(2,0).问:是否存在这样的直线
与该抛物线交于点P,与直线AC交于点F,点D的坐标为(2,0).问:是否存在这样的直线 ,使得△ODF是等腰三角形?若存在,请求出点P的坐标;若不存在,请说明理由。
,使得△ODF是等腰三角形?若存在,请求出点P的坐标;若不存在,请说明理由。
1.(1)由题意,得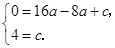 ……………………………………1分[来源:Z+xx+k.Com]
……………………………………1分[来源:Z+xx+k.Com]
解得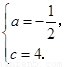
 所求二次函数的关系式为:
所求二次函数的关系式为: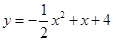 .……………2分
.……………2分
2.(2)对称轴为直线x=1,顶点坐标为(1,4.5)…………………………………… 4分
3.(3)设点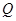 的坐标为
的坐标为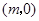 ,过点
,过点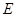 作
作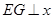 轴于点
轴于点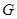 .
.
 由
由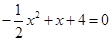 ,得
,得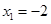 ,
,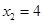 .
.
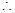 点
点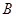 的坐标为
的坐标为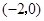 .……………………………5分
.……………………………5分
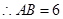 ,
,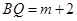 .
.
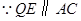 ,
,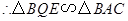 .
.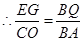 ,
,
即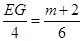 .
. .…………………6分
.…………………6分
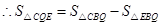
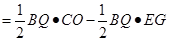

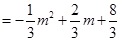
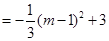 .……………………………………7分
.……………………………………7分
又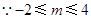 ,
,
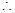 当
当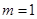 时,
时,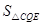 有最大值3,此时
有最大值3,此时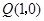 .……………………………………8分
.……………………………………8分
4.(3)存在.
在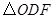 中.
中.
(ⅰ)若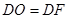 ,
,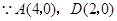 ,
,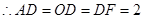 .
.
又在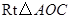 中,
中,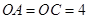 ,
,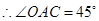 .
.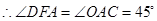 .
.
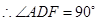 .此时,点
.此时,点 的坐标为
的坐标为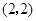 .
.
由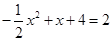 ,得
,得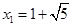 ,
,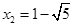 .
.
此时,点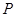 的坐标为:
的坐标为: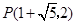 或
或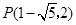 .………………………………10分
.………………………………10分
(ⅱ)若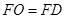 ,过点
,过点 作
作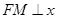 轴于点
轴于点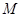 ,
,
由等腰三角形的性质得: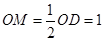 ,
,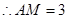 ,[来源:Z&xx&k.Com]
,[来源:Z&xx&k.Com]
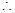 在等腰直角
在等腰直角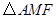 中,
中,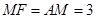 .
.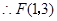 .
.
由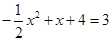 ,得
,得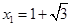 ,
,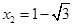 .
.
此时,点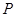 的坐标为:
的坐标为: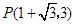 或
或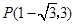 .……………………………
…11分
.……………………………
…11分

【解析】略


 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案科目:初中数学 来源: 题型:
(本题12分)已知二次函数的图象经过点(0,-3),且顶点坐标为(-1,-4).
(1)求该二次函数的解析式;
(2)设该二次函数的图象与x轴的交点为A、B,与y轴的交点为C,求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源:2011年江苏省沭阳县中学中考模拟考试数学卷.doc 题型:解答题
﹣(本题12分)已知二次函数y=x2+bx+c与x轴交于A(-1,0)、B(1,0)两点.
(1)求这个二次函数的关系式;
(2)若有一半径为r的⊙P,且圆心P在抛物线上运动,当⊙P与两坐标轴都相切时,求半径r的值.
(3)半径为1的⊙P在抛物线上,当点P的纵坐标在什么范围内取值时,⊙P与y轴相离、相交?
查看答案和解析>>
科目:初中数学 来源:011-2012学年山西省大同市九年级上学期第一次月考数学卷 题型:填空题
(本题12分)已知两个全等的直角三角形纸片ABC、DEF,如图(1)放置,点B、D重合,点F在BC上,AB与EF交于点G,∠C=∠EFB=90°,∠E=∠ABC=30°,AB=DE=4.

1.(1)求证:△EGB是等腰三角形
2.(2)若纸片DEF不动,问△ABC绕点F逆时针旋转最小 度时,四边形ACDE成为以ED为底的梯形(如图(2)),求此梯形的高。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com